 Multiple Choice Questions
Multiple Choice QuestionsLet α and β be the distinct roots of ax2 + bx + c = 0, then 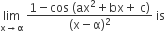  equal to
 equal to
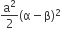
0
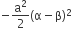
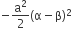
A.
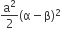
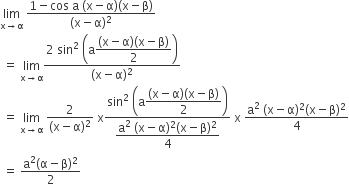
If x is so small that x3 and higher powers of x may be neglected, then 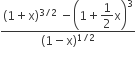 may be approximated as
may be approximated as
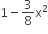
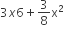
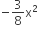
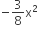
If both the roots of the quadratic equation x2 – 2kx + k2 + k – 5 = 0 are less than 5, then k lies in the interval
(5, 6]
(6, ∞)
(-∞, 4)
(-∞, 4)
If the equation anxn +an-1xn-1 +....... +a1x =0, a1 ≠0, n≥2, has a positive root x = α, then the equation nanxn-1 + (n-1)an-1xn-2 +......+a1 = 0 has a positive root, which is
greater than α
smaller than α
greater than or equal to α
greater than or equal to α
Let z, w be complex numbers such that z iw + = 0 and arg zw = π. Then arg z equals
Ï€/4
5Ï€/4
3Ï€/4
3Ï€/4
If (1 – p) is a root of quadratic equation x2 +px + (1-p)=0 , then its roots are
0, 1
-1, 2
0, -1
0, -1
If one root of the equation x2+px+12 =0 is 4, while the equation x2 +px +q = 0 has equal roots, then the value of 'q' is
49/3
4
3
3
The coefficient of xn in expansion of (1+x)(1-x)n is
(n-1)
(-1)n(1-n)
(-1)n-1(n-1)2
(-1)n-1(n-1)2
If 2a + 3b + 6c =0, then at least one root of the equation ax2Â + bx+ c = 0Â lies in the interval
(0,1)
(1,2)
(2,3)
(2,3)
