 Multiple Choice Questions
Multiple Choice QuestionsConsider a two-particle system with particles having masses m1 and m2. If the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle be moved, so as to keep the centre of mass at the same position?
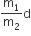
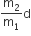
d
d
An annular ring with inner and outer radii R1 and R2 is rolling without slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, F1/F2 is
R1/R2
(R1/R2)2
1
1
A smooth block is released at rest on a 45° incline and then slides a distance d. The time taken to slide is n times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
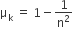
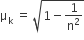
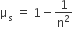
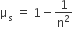
The upper half of an inclined plane with inclination φ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
2sinφ
2cosφ
A bullet fired into a fixed target loses half of its velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
3.0 cm
2.0 cm
1.5 cm
1.5 cm
Out of the following pair, which one does NOT have identical dimensions is
angular momentum and Planck’s constant
impulse and momentum
moment of inertia and moment of a force
moment of inertia and moment of a force
A body A of mass M while falling vertically downwards under gravity breaks into two parts; a body B of mass 1/3 M and a body C of mass 2/3 M. The centre of mass of bodies B and C taken together shifts compared to that of body A towards
depends on height of breaking
does not shift
body C
body C
A particle of mass 0.3 kg is subjected to a force F=−kx with k=15 N/m. What will be its initial acceleration if it is released from a point 20 cm away from the origin?
3 m/s2
15 m/s2
5 m/s2
5 m/s2
The block of mass M moving on the frictionless horizontal surface collides with a spring of spring constant K and compresses it by length L. The maximum momentum of the block after collision is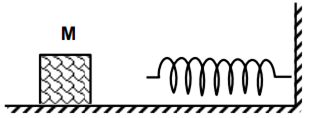

KL2/2M
zero
zero
A mass ‘m’ moves with a velocity v and collides inelastically with another identical mass. After collision, the 1st mass moves with velocity v/√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision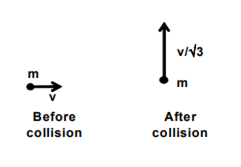
v
√3 v
2v/√3
2v/√3
