 Multiple Choice Questions
Multiple Choice QuestionsA red LED emits light at 0.1 watt uniformly around it. The amplitude of the electric field of the light at a distance of 1 m from the diode is:
1.73 V/m
2.45 V/m
5.48 V/m
5.48 V/m
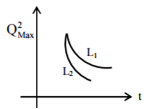
An LCR circuit is equivalent to a damped pendulum. In an LCR circuit, the capacitor is charged to Q0 and then connected to the L and R as shown.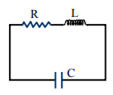
If a student plots graphs of the square of maximum charge ( QMax2 ) on the capacitor with time (t) for two different values L1 and L2 (L1 > L2) of L then which of the following represents this graph correctly? (Plots are schematic and not drawn to scale)
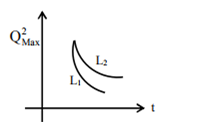
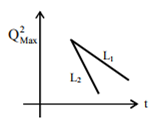
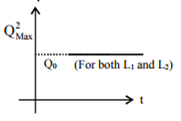
In a large building, there are 15 bulbs of 40 W, 5 bulbs of 100 W, 5 fans of 80 W and 1 heater of 1kW. The voltage of the electric mains is 220 V. The minimum capacity of the main fuse of the building will be
8 A
10 A
12 A
12 A
A conductor lies along the z-axis at -1.5 ≤ z< 1.5 m and carries a fixed current of 10.An in-az direction (see figure).
B = 3.0 x 10-4 e-0.2x ay T, find the power required to move the conductor at constant speed to x = 2.0 , y = 0 in 5 x10-3 s. Assume parallel motion along the x axis.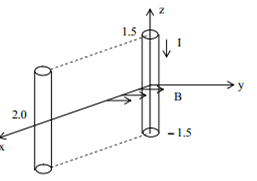
1.57 W
2.97 W
04.85 W
04.85 W
In an LCR circuit as shown below both switches are open initially. Now switch S1 is closed, S2 kept open. (q is charge on the capacitor and τ = RC is capacitive time constant). Which of the following statement is correct?
Work done by the battery is half of the energy dissipated in the resistor
At t = τ, q = CV/2
At t = 2τ, q = CV (1-e-2)
At t = 2τ, q = CV (1-e-2)
A current I flows in an infinitely long wire with cross-section in the form of a semicircular ring of radius R. The magnitude of the magnetic induction along its axis is




A resistor R and 2 μF capacitor in series connected through a switch to 200 V direct supply. Across the capacitor is a neon bulb that lights up at 120 V. Calculate the value of R to make the bulb light up 5 s after the switch has been closed. (log10 2.5 = 0.4)
1.7 x 105 Ω
2.7 x 106 Ω
3.3 x 107 Ω
3.3 x 107 Ω
In a series LCR circuit, R = 200 Ω and the voltage and the frequency of the main supply is 220 V and 50 Hz respectively. On taking out the capacitance from the circuit the current lags behind the voltage by 30º. On taking out the inductor from the circuit the current leads the voltage by 30º. The power dissipated in the LCR circuit is
305 W
210 W
zero
zero
In an a.c. circuit the voltage applied is E = E0 sinπt. The resulting current in the circuit is I = I0 sin 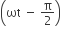 .The power consumption in the circuit is given by
.The power consumption in the circuit is given by
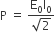
P = zero
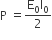
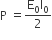
A current I flows along the length of an infinitely long, straight, thin walled pipe. Then
the magnetic field is zero only on the axis of the pipe
the magnetic field is different at different points inside the pipe
the magnetic field at any point inside the pipe is zero
the magnetic field at any point inside the pipe is zero
