 Multiple Choice Questions
Multiple Choice QuestionsThe system of linear equations x+λy−z=0; λx−y−z=0; x+y−λz=0 has a non-trivial solution for
infinitely many values of λ.
exactly one value of λ.
exactly two values of λ.
exactly two values of λ.
A = 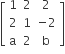 is a matrix satisfying the equation AAT = 9I, Where I is 3 x 3 identity matrix, then the ordered pair (a,b) is equal to
is a matrix satisfying the equation AAT = 9I, Where I is 3 x 3 identity matrix, then the ordered pair (a,b) is equal to
(2,-1)
(-2,1)
(2,1)
(2,1)
The set of all values of λ for which the system of linear equations
2x1-2x2+x3 = λx1
2x1- 3x2 + 2x3 = λx2
-x1 + 2x2 = λx3
a non- trivial solution.
is an empty set
is a singleton set
contains two elements
contains two elements
If α, β ≠ 0 and f(n) = αn+ βn and 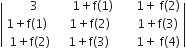
= K(1-α)2(1-β)2(α- β)2, then K is equal to
αβ
1/αβ
1
1
If A is a 3x3 non- singular matrix such that AAT = ATA, then BBT is equal to
B-1
B-1
Let P and Q be 3 × 3 matrices with P ≠ Q. If P3= Q3 and P2Q = Q2P, then determinant of(P2+ Q2) is equal to
-2
1
0
0
The number of values of k for which the linear equations
4x + ky + 2z = 0
kx + 4y + z = 0
2x + 2y + z = 0
posses a non-zero solution is:
3
2
1
1
Consider the system of linear equation
x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
The system has
infinite number of solutions
exactly 3 solutions
a unique solution
a unique solution
Let A be a 2 × 2 matrix with non-zero entries and let A2 = I, where I is 2 × 2 identity matrix. Define Tr(A) = sum of diagonal elements of A and |A| = determinant of matrix A.
Statement-1: Tr(A) = 0.
Statement-2: |A| = 1.
Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is true; statement-2 is not a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is false.
Statement-1 is true, Statement-2 is false.
