CBSE Gujarat Board Haryana Board
Class 10 Class 12
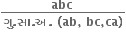
આપણે જાણીએ છીએ કે, કોઈ પણ અયુગ્મ પૂર્ણાંક a એ a=4k+1 અથવા a=4k+3 સ્વરૂપમાં હોય છે.
જ્યાં kεZ 
a2 = (4k + 1)2 અથવા a2 = (4k + 3)2 
a2 = 16k2 + 8k અથવા a2 = 16k2 + 24k + 9 
a2-1 = 16k + 8k અથવા a2-1 = 16k2 + 24k + 8 
a2 - 1 = 2(2k2 + k) અથવા a2-1 = (2k2 + 3k + 1)
આમ, a2 - 1 એ 8 વડે વિભાજ્ય છે. 
અયુગ્મ પૂર્ણાંકના વર્ગમાંથી 1 બાદ કરતાં મળતો પૂર્ણાંક 8 નો ગુણિત થાય છે.
બીજી રીત :
ભાગ-પ્રવિધિ પ્રમાણે કોઈ પણ પૂર્ણાંક a માટે,
a = bk + r જ્યાં, kεz તથા =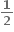 
< r 
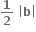
અહીં, b=4 લેતાં,
a = 4k + r જ્યાં, kεZ તથા -2 < r 
2 (
b = 4 માટે -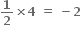 
)
હવે, -2 < r 
2 એટલે કે,
r = -1 અથવા 0 અથવા 1 અથવા 2
પરંતું એ અયુગ્મ સંખ્યા છે. 
r = 0 અને r = 2 શક્ય નથી.
આથી a = 4k + (-1) અથવા a = 4K + 1, kεZ
a = 4k+1 
a2 + (4k+1)2
a2 - 1 = 8 (2k + k)
આમ, a2 - 1 એ 8 વડે વિભાજ્ય છે. 
અયુગ્મ પૂર્ણાંકના વર્ગમાંથી 1 બાદ કરતાં મળતો પૂર્ણાંક 8 નો ગુણિત થાય છે.
અસંમેય છે.
