CBSE Gujarat Board Haryana Board
Class 10 Class 12
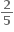ગણા હોય. 
આપેલ છે. 
ના ત્રણ એકરૂપ ભાગ કરવાના છે.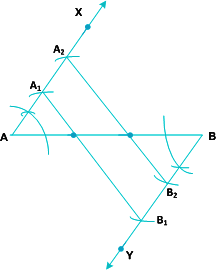 
ના ભિન્ન અર્ધતલમાં 
અને 
દોરીએ. કે જેહી લઘુકોણો ∠XAB તથા ∠YBA મળે અને 
. 
ને A1માં છેદતું બીજું એક ચાપ દોરીએ. આ જ પ્રમાણે આટલી જ ત્રિજ્યા રખી A1ને કેન્દ્ર લઈ 
ને A2માં છેદતું બીજું એક ચાપ એવી રીતે દોરીએ કે જેથી A-A1-A2 થાય. અહીં, AA1 = A1A2 થશે. 
ને B1માં છેદતું એક ચાપ દોરીએ. ફરીથી B1ને કેન્દ્ર લઈ અને આ જ ત્રિજ્યા રાખી 
ને B2માં છેદતું એક ચાપ દોરીએ કે જેથી B-B1-B2 થાય. અહીં, પણ BB1 = B1B2 થશે. 
તથા 
એવાં દોરીએ, કે જેથી તે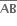 
ને અનુક્રમે P તથા Qમાં છેદે. 
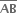ને ત્રણ એકરૂપ ભાગમાં વિભાજીત કરે છે. એટલે કે AP = PQ = QB = 
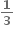AB. 
