વર્તુળના કેન્દ્ર Oમાંથી પસાર થતી એક રેખા વર્તુળના એક સ્પર્શકને Qબિંદુમાં છેદે છે. સ્પર્શકનું સ્પર્શબિંદુ P છે. વર્તુળની ત્રિજ્યા 5 હોય અને OQ = 13 હોય, તો PQ શોધો. from ગણિત વર્તુળ Class 10 GSEB

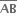$top enclose bold AB$ એક વર્તુળનો વ્યાસ છે. સાબિત કરો કે, A અને B બિંદુએ વર્તુળને દોરેલા સ્પર્શકો પરસ્પર સમાંતર છે.

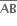A અને B એક વર્તુળ પરનાં બે ભિન્ન બિંદુઓ છે, જેથી $top enclose bold AB$ વ્યાસ નથી. A અને B બિંદુએ વર્તુળને દોરેલા સ્પર્શકો P બિંદુમાં છેદે છે. સાબિત કરો કે, ∠AOB અને ∠APB એકબીજાના પૂરકકોણો છે. ઉપરાંત સાબિત કરો કે, PA = PB.

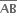એક વર્તુળ ∆ABCની બાજુઓ $top enclose bold BC bold comma bold space top enclose bold CA bold comma bold space top enclose bold AB bold space$ ને અનુક્રમે D, E, Fમાં સ્પર્શે છે. વર્તુળની ત્રિજ્યા 4 એકમ છે. જો BD = 8, DC = 6 હોય તો, AB અને AC શોધો.

$bold circled dot$ (O, r₁) અને ⊙(O, r₂) બે સમકેન્દ્રીદ્રી વર્તુળો છે, જેમાં r₁ > r₂. ⊙(O, r₂) ની જીવા $top enclose top enclose bold AB end enclose$ એ ⊙ (O, r₂) ને P બિંદુએ સ્પર્શે છે. સાબિત કરો કે, P એ $top enclose bold AB$ નું મધ્યબિંદુ છે.

વર્તુળના કેન્દ્ર Oમાંથી પસાર થતી એક રેખા વર્તુળના એક સ્પર્શકને Qબિંદુમાં છેદે છે. સ્પર્શકનું સ્પર્શબિંદુ P છે. વર્તુળની ત્રિજ્યા 5 હોય અને OQ = 13 હોય, તો PQ શોધો.

O વર્તુળનું કેન્દ્ર છે અને સ્પર્શકનું સ્પર્શબિંદુ P છે.

∴ OP = વર્તુળની ત્રિજ્યા

∴ OP = 5, OQ = 13

અને ∠OPQ કાટ્ખૂણો છે, કારણ કે સ્પર્શકના સ્પર્શબિંદુએ દોરેલી ત્રિજ્યા સ્પર્શકને લંબ હોય.

∴ ∆OPQ માં, OP² + PQ² = OQ²

∴ 5² + PQ² = 13²

∴ PQ² = 13² - 5²

= 169 - 25 = 144

∴ PQ = 12

Chapter Chosen

Book Chosen

Subject Chosen

Book Store

Previous Year Papers

વર્તુળ

Switch