CBSE Gujarat Board Haryana Board
Class 10 Class 12
 મધ્યગાઓ છે. સાબિત કરો કે, 4(AD2 + BE2 + CF2) = 3(AB2 + BC2 + AC2).
મધ્યગાઓ છે. સાબિત કરો કે, 4(AD2 + BE2 + CF2) = 3(AB2 + BC2 + AC2).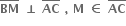 જો AM = 4MC, તો સાબિત કરો કે, AB = 2BC.
જો AM = 4MC, તો સાબિત કરો કે, AB = 2BC. 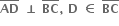 તો સાબિત કરો કે,
તો સાબિત કરો કે, 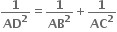
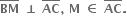 જો AM = x, BM = y તો AB, BC અને CM ને x અને y ના સ્વરૂપમાં મેળવો. (x > 0, y > o)
જો AM = x, BM = y તો AB, BC અને CM ને x અને y ના સ્વરૂપમાં મેળવો. (x > 0, y > o) એક વેધ છે અને M
એક વેધ છે અને M  . જો QM = 12, PR = 26, તો PM અને RM શોધો. જો PM < RM, તો Pq અને QR શોધો.
. જો QM = 12, PR = 26, તો PM અને RM શોધો. જો PM < RM, તો Pq અને QR શોધો. 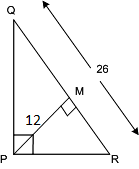
 વેધ છે.
વેધ છે. 
