 Multiple Choice Questions
Multiple Choice QuestionsA mass m moving horizontally (along the x -axis) with velocity v collides and sticks to mass of 3m moving vertically upward (along the y -axis) with velocity 2v. The final velocity of the combination
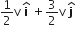
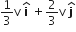
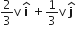
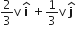
A block of mass m is in contact with the cart C as shown in the figure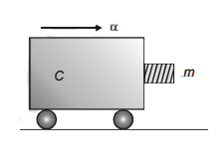
The coefficient of static friction between the block and the cart is μ. The acceleration α of the cart that will prevent the block from falling satisfies


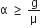
A ball moving with velocity 2 ms-1 collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms-1) after collision will be
0,1
1,1
1,0.5
1,0.5
A man of 50 kg mass standing in a gravity free space at height of 10 m above the floor. He throws a stone of 0.5 kg mass downwards with a speed 2 ms-1. When the stone reaches the floor, the distance of the man above the floor will be
9.9 m
10.1
10 m
10 m
A student measures the distance traversed in free fall of a body, initially at rest in a given time. He uses this data to estimate g, the acceleration due to gravity. If the maximum percentage errors in measurement of the distance and the time are e1 and e2 respectively, the percentage error in the estimation of g is
e1 - e2
e1 + 2e2
e1+ e2
e1+ e2
An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are 1 kg first part moving with a velocity of 12 ms-1 and 2 kg second part moving with a velocity of 8 ms-1.If the third part flies off with a velocity of 4 ms-,its mass would be
5 kg
7 kg
17 kg
17 kg
The mass of a lift is 2000 kg. When the tension in the supporting cable is 28000 N, then its acceleration is
30 ms-2 downward
4 ms-2 upwards
4 ms-2 downwards
4 ms-2 downwards
A body under the action of a force, acquires an acceleration of 1 ms-2. The mass of this body must be
acquires an acceleration of 1 ms-2. The mass of this body must be

20 kg
10 kg
10 kg
A closed loop PQRS carrying a current is placed in a uniform magnetic field. If the magnetic forces on segments PS, SR and RQ are F1, F2 and F3 respectively and are in the plane of the paper and along the directions shown, the force on the segment of QP is
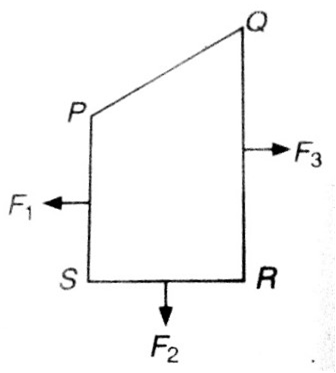
F3 - F1-F2
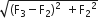
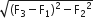
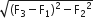
Three forces acting on a body are shown in the figure. To have the resultant force only along the y-direction, the magnitude of the minimum additional force needed is
0.5 N
1.5 N


