 Multiple Choice Questions
Multiple Choice QuestionsA car of mass 1000 kg negotiates a banked curve of radius 90m on a frictionless road. If the banking angle is 45o, the speed of the car is
20 ms-1
30ms-1
5 ms-1
5 ms-1
Two sphere A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along the x -axis. After the collision, B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
same as that of B
opposite to that of B
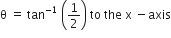
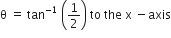
The upper half of an inclined plane of the inclination  is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by,
is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by,
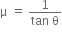
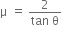


An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12 m/s and the second part of mass 2 kg moves with second part of mass 2 kg moves with 8 m/s speed. If the third part flies off with 4 m/s speed, then its mass is,
3 kg
5 kg
7 kg
7 kg
A person of mass 62 kg is inside of a lift of mass 940 kg and presses the button on control panel. The lift starts moving upwards with an acceleration 1.0 m/s2. If g = 10 m/s2 ,the tension in the supporting cable is
9680 N
11000 N
1200 N
1200 N
A planet moving along an elliptical orbit is closer to the sun at a distance r1 and farthest away at a distance of r2. if v1 and v2 are the linear velocities at these points respectively, then the ratio v1/v2 is
r2/r1
(r2/r1)2
r1 /r2
r1 /r2
Force F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12 m is
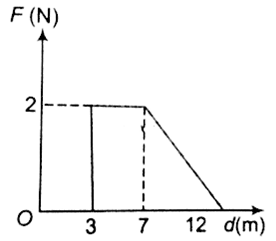
21 J
26 J
13 J
13 J
Uniform magnetic field acting along AB. If the magnetic force on the arm BC Is F, the force on the arm AC is
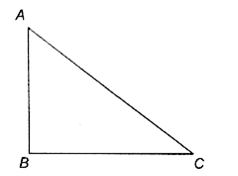


Two stone of masses m and 2m are whirled in horizontal circles, the heavier one in a radius r/2 and the lighter one in radius r. The tangential speed of lighter one in radius r. The tangential speed of lighter stone is n times that of the value of heavier stone when they experience same centripetal forces. The value of n is
2
3
4
4
Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats/s when both the wires oscillate together would be
0.02
0.03
0.04
0.04
