 Multiple Choice Questions
Multiple Choice QuestionsThe electric field of an electromagnetic wave in free space is given by 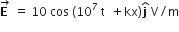 , where t and x are in seconds and meters respectively. It can be inferred that
, where t and x are in seconds and meters respectively. It can be inferred that
1) the wavelength λ is 188.4 m.
2)The wave number k is 0.33 rad/m.
3)The wave amplitude is 10 V /m.
4)The wave is propagating along +x direction
(3) and (4)
(1) and (2)
(2) and (3)
(2) and (3)
The electric potential at a point (x, y, Z) is given by
V = - x2y -xz3 + 4
The electric field E at that point is
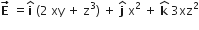
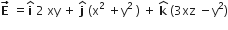
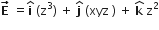
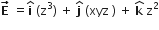
A hollow cylinder has to charge q coloumb within it. Φ is the electric flux in a unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in a unit of voltmeter will be:
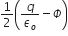
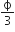
In a discharge tube ionization of enclosed gas is produced due to collisions between
positive ions and neutral atoms/molecules
negative electrons and neutral atoms/molecules
photons and neutral atoms/molecules
photons and neutral atoms/molecules
A square surface of side L m is in the plane of the paper. A uniform electric field 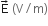 , also in the plane of the paper, is limited only to the lower half of the square surface, (see figure). The electric flux in SI units associated with the surface is
, also in the plane of the paper, is limited only to the lower half of the square surface, (see figure). The electric flux in SI units associated with the surface is
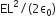

zero
zero
An electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. The direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall of the proton is
Smaller
5 times greater
Equal
10 times greater
A certain charge Q is divided into two parts q and Q-q. How the charge Q and q must be related so that when q and (Q-q) is placed at a certain distance apart experience maximum electrostatic repulsion?
Q = 2q
q = 3q
Q = 4q
Q= 4q + c
A charged particle 'q' is shot with speed v towards another fixed charged particle Q. It approaches Q upto the closest distance r and then returns. If q were given a speed 2v, the closest distance of approach would be
![]()
r
2r
r/2
r/4
A conducting sphere of radius R = 20 cm is given by a charge Q = 16μC. What is E at centre?
3.6×106 N/C
1.8×106 N/C
Zero
0.9×106 N/C
If an insulated non-conducting sphere of radius R has charge density ρ. The electric field at a distance r from the centre of sphere (r > R) will be
