Short Answer TypeState the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies.
Cyclotron works on the principle that an oscillating electric field can be used to accelerate a charge particle to high energy.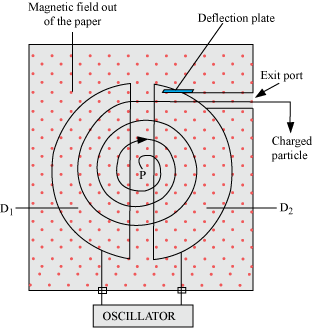
In a cyclotron, the charged particles across the gap between the two D-shaped magnetic field regions are accelerated by an electric field. The magnetic field is perpendicular to the paths of the charged particles that make them follow circular paths within the two Dee’s. An alternating voltage accelerates the charged particles each time they cross the Dee’s. The radius of each particle’s path increases with its speed. So, the accelerated particles spiral toward the outer wall of the cyclotron.
The accelerating electric field reverses just at the time the charge particle finishes its half circle so that it gets accelerated across the gap between the Dee’s. The particle gets accelerated again and again, and its velocity increases. Therefore, it attains high kinetic energy.
An electric dipole of length 4 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of 4 Nm. Calculate the potential energy of the dipole, if it has charge ±8 n C.
A potentiometer wire of length 1 m has a resistance of 10 Ω. It is connected to a 6 V battery in series with a resistance of 5 Ω. Determine the emf of the primary cell which gives a balance point at 40 cm.
(a) Obtain the expression for the energy stored per unit volume in a charged parallel plate capacitor.
(b) The electric field inside a parallel plate capacitor is E. Find the amount of work done in moving a charge q over a closed loop a b c d a.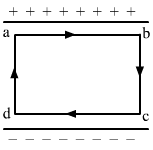
(a) State Ampere's circuital law, expressing it in the integral form.
(b) Two long coaxial insulated solenoids, S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current 'I' flow thought the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current 'I' flows in the opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point
(i) Inside on the axis, and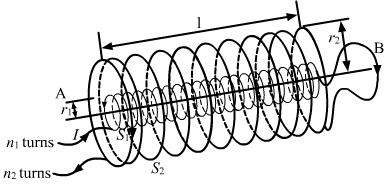
Answer the following:
(a) Name the EM waves which are suitable for radar systems used in aircraft navigation. Write the range of frequency of these waves.
(b) If the earth did not have atmosphere, would its average surface temperature be higher or lower than what it is now? Explain.
(c) An EM wave exerts pressure on the surface on which it is incident. Justify.A convex lens is placed in contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens?
The figure given below shows the block diagram of a generalized communication system. Identify the element labelled 'X' and write its function.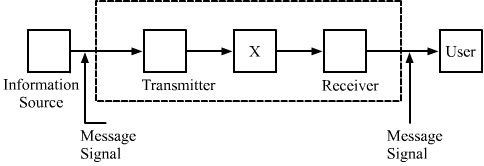
For a single slit of width "a", the first minimum of the interference pattern of a monochromatic light of wavelength λ occurs at an angle of 
. At the same angle of 
, we get a maximum for two narrow slits separated by a distance "a". Explain.
Switch
