 Multiple Choice Questions
Multiple Choice QuestionsLet z, w be complex numbers such that z iw + = 0 and arg zw = π. Then arg z equals
π/4
5π/4
3π/4
3π/4
C.
3π/4
Since z + iw = 0 ⇒ z = −iw
⇒ z = iw
⇒ w = -iz
Also arg(zw) = π
⇒ arg (-iz2) = π
⇒ arg (-i) + 2 arg(z) = π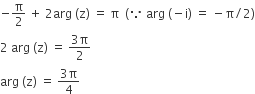
If a1, a2, a3 , ....,an , .... are in G.P., then the value of the determinant 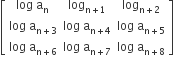 is
is
0
-2
1
1
Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation
x2 + 18x +16 = 0
x2-18x-16 = 0
x2+18x-16 =0
x2+18x-16 =0
If (1 – p) is a root of quadratic equation x2 +px + (1-p)=0 , then its roots are
0, 1
-1, 2
0, -1
0, -1
Let S(K) = 1 +3+5+..... (2K-1) = 3+K2. Then which of the following is true?
S(1) is correct
Principle of mathematical induction can be used to prove the formula
S(K) ≠S(K+1)
S(K) ≠S(K+1)
How many ways are there to arrange the letters in the word GARDEN with the vowels in alphabetical order?
120
480
360
360
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is
5
38
38
If one root of the equation x2+px+12 =0 is 4, while the equation x2 +px +q = 0 has equal roots, then the value of 'q' is
49/3
4
3
3
