 Multiple Choice Questions
Multiple Choice QuestionsIn a geometric progression consisting of positive terms, each term equals the sum of the next two terms. Then the common ratio of this progression equals
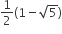
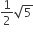


D.

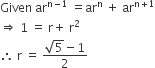
In the binomial expansion of (a - b)n, n ≥ 5, the sum of 5th and 6th terms is zero, then
a/b equals
5/n −4
6 /n −5
n -5 /6
n -5 /6
The set S: {1, 2, 3, …, 12} is to be partitioned into three sets A, B, C of equal size. Thus, A ∪ B ∪ C = S, A ∩ B = B ∩ C = A ∩ C = φ. The number of ways to partition S is-
12!/3!(4!)3
12!/3!(3!)4
12!/(4!)3
12!/(4!)3
A body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are
12 kg and 13 kg
5 kg and 5 kg
5 kg and 12 kg
5 kg and 12 kg
Consider a family of circles which are passing through the point (-1, 1) and are tangent to x-axis. If (h, K) are the co-ordinates of the centre of the circles, then the set of values of k is given by the interva
0 < k < 1/2
k ≥ 1/2
– 1/2 ≤ k ≤ 1/2
– 1/2 ≤ k ≤ 1/2
The differential equation of all circles passing through the origin and having their centres on the x-axis is
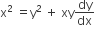
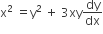
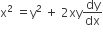
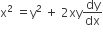
If p and q are positive real numbers such that p2 + q2 = 1, then the maximum value of (p + q) is
2
1/2
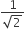
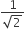
A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (= a) subtends an angle of 60º at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30º. The height of the tower is




