Multiple Choice QuestionsOne ticket is selected at random from 50 tickets numbered 00, 01, 02, ... , 49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
1/14
1/7
5/14
5/14
A.
1/14
A = Events that sum of the digits on selected ticket is 8
= {08, 17, 26, 35, 44}
n(A) = 5
Event that product of digits is zero
= {00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 20,30, 40}
⇒ n(B) = 14
=P(A/B) = (5/14)
Statement 1: ~ (p ↔ ~ q) is equivalent to p ↔ q
Statement 2 : ~ (p ↔ ~ q) is a tautology
Statement–1 is true, Statement–2 is true, Statement–2 is a correct explanation for statement–1
Statement–1 is true, Statement–2 is true; Statement–2 is not a correct explanation for statement–1.
Statement–1 is true, statement–2 is false.
Statement–1 is true, statement–2 is false.
Statement 1: The variance of first n even natural numbers is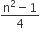 
Statement 2: The sum of first n natural numbers is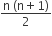 
and the sum of squares of first n natural numbers is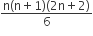 
Statement–1 is true, Statement–2 is true, Statement–2 is a correct explanation for statement–1
Statement–1 is true, Statement–2 is true; Statement–2 is not a correct explanation for statement–1.
Statement–1 is true, statement–2 is false.
Statement–1 is true, statement–2 is false.
Let a, b, c be such that 0 (a +c) ≠ . If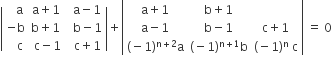 
,then the value of 'n' is
0
any even integer
any odd integer
any odd integer
For real x, let f(x) = x3+ 5x + 1, then
f is one–one but not onto R
f is onto R but not one–one
f is one–one and onto R
f is one–one and onto R
Let y be an implicit function of x defined by x2x – 2xxcoty – 1 = 0. Then y′ (1) equals
-1
1
log 2
log 2
Given P(x) = x4+ ax3 + cx + d such that x = 0 is the only real root of P′ (x) = 0. If P(–1) < P(1),then in the interval [–1, 1].
P(–1) is the minimum and P(1) is the maximum of P
P(–1) is not minimum but P(1) is the maximum of P
P(–1) is the minimum but P(1) is not the maximum of P
P(–1) is the minimum but P(1) is not the maximum of P
Let f(x) = (x + 1)2– 1, x ≥ – 1
Statement – 1: The set {x : f(x) = f–1(x)} = {0, –1}.
Statement – 2: f is a bijection.
Statement–1 is true, Statement–2 is true,Statement–2 is a correct explanation for statement–1
Statement–1 is true, Statement–2 is true; Statement–2 is not a correct explanation for statement–1.
Statement–1 is true, statement–2 is false.
Statement–1 is true, statement–2 is false.
Let f(x) = x|x| and g(x) = sinx
Statement 1 : gof is differentiable at x = 0 and its derivative is continuous atthat point
Statement 2: gof is twice differentiable at x = 0
Statement–1 is true, Statement–2 is true, Statement–2 is a correct explanation for statement–1
Statement–1 is true, Statement–2 is true;Statement–2 is not a correct explanation for statement–1.
Statement–1 is true, statement–2 is false.
Statement–1 is true, statement–2 is false.
Switch
[cot x]dx, where [.] denotes the greatest integer function, is equal to
