 Multiple Choice Questions
Multiple Choice QuestionsConsider the following relations:
R = {(x, y)| x, y are real numbers and x = wy for some rational number w}; S = {(m/p, p/q)| m, n, p and q are integers such that n, q ≠ 0 and qm = pn}. Then
R is an equivalence relation but S is not an equivalence relation
neither R nor S is an equivalence relation
S is an equivalence relation but R is not an equivalence relation
S is an equivalence relation but R is not an equivalence relation
D.
S is an equivalence relation but R is not an equivalence relation
A person is to count 4500 currency notes. Let a denote the number of notes he counts in the nth minute. If a1 = a2 = ... = a10 = 150 and a10, a11, ...are in an AP with common difference -2, then the time taken by him to count all notes is
24 min
34 min
125 min
125 min
The equation of the tangent to the curve y = x +4/x2, that is parallel to the x-axis, is
y= 0
y= 1
y= 2
y= 2
Let p(x) be a function defined on R such that 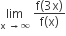 = 1, p'(x) p'(1-x),for all x∈[0,1] p(0) = 1 and p(1) = 41. Then
= 1, p'(x) p'(1-x),for all x∈[0,1] p(0) = 1 and p(1) = 41. Then 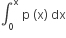 equals
equals
√41
21
41
41
Let S be a non empty subset of R. Consider the
following statement:
P: There is a rational number x∈S such that x > 0.
Which of the following statements is the negation of the statement P?
There is a rational number x∈S such that x ≤ 0.
There is no rational number x∈ S such that x≤0.
Every rational number x∈S satisfies x ≤ 0.
Every rational number x∈S satisfies x ≤ 0.
Let cos (α + β) = 4/5 and let sin (α - β) = 5/13, where 0 ≤α,β ≤ π/4. Then tan 2α is equal to
25/16
56/33
19/12
19/12
For two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is
5/2
11/2
6
6
For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is
there is a regular polygon with r/R = 1/2
there is a regular polygon with 
there is a regular polygon with r/R = 2/3
there is a regular polygon with r/R = 2/3
