11.

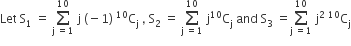
Statement-1: S₃ = 55 × 2⁹.
Statement-2: S₁ = 90 × 2⁸ and S2 = 10 × 2⁸.

• Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is true; statement-2 is not a correct explanation for Statement-1. 

• Statement-1 is true, Statement-2 is false.

• Statement-1 is true, Statement-2 is false.

Consider the system of linear equation
x¹ + 2x² + x³ = 3
2x¹ + 3x² + x³ = 3
3x¹ + 5x² + 2x³ = 1
The system has

• infinite number of solutions

• exactly 3 solutions

• a unique solution

• a unique solution

let f : (-1, 1) → R be a differentiable function
with f(0) = -1 and f'(0) = 1.
Let g(x) = [f(2f(x) + 2)]². Then g'(0) =

• 4

• -4

• 0

• 0

Let f : R → R be a positive increasing function with 

• 1

• 2/3

• 3/2

• 3/2

Let A be a 2 × 2 matrix with non-zero entries and let A2 = I, where I is 2 × 2 identity matrix. Define Tr(A) = sum of diagonal elements of A and |A| = determinant of matrix A.
Statement-1: Tr(A) = 0.
Statement-2: |A| = 1.

• Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is true; statement-2 is not a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is false.

• Statement-1 is true, Statement-2 is false.

Let f : R → R be a continuous function defined
by f(x) = 1/e^x + 2e^-x
Statement - 1: f(c) = 1/3, for some c ∈ R.
Statement-2: 0 < f(x)≤ 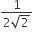, for all x ∈ R.

• Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is true; statement-2 is not a correct explanation for Statement-1.

• Statement-1 is true, Statement-2 is false.

• Statement-1 is true, Statement-2 is false.

The equation of the tangent to the curve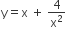, that is parallel to the x-axis, is

• y = 0

• y = 1

• y = 3

• y = 3

If two tangents drawn from a point P to the parabola y²= 4x are at right angles, then the locus of P is

• X = 1

• 2x +1 = 0

• x = -1

• x = -1

The number of 3 × 3 non-singular matrices, with four entries as 1 and all other entries as 0, is 

• less than 4

• 5

• 6

• 6

Let f : R → R be defined by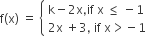

If f has a local minimum at x = - 1 then a possible value of k is

• 1

• 0

• -1/2

• -1/2