 Multiple Choice Questions
Multiple Choice QuestionsLet α, β be real and z be a complex number. If z2 + αz + β = 0 has two distinct roots on the line Re z = 1, then it is necessary that
β ∈(0, 1)
β ∈(-1, 0)
|β| = 1
|β| = 1
D.
|β| = 1
Let roots be p + iq and p - iq p, q ∈ R
root lie on line Re(z) = 1
⇒ p = 1
product of roots = p2 + q2 = β = 1 + q2
⇒ β∈ (1, ∞), (q ≠ 0, ∵ roots are distinct)
A man saves Rs. 200 in each of the first three months of his service. In each of the subsequent months his saving increases by Rs. 40 more than the saving of immediately previous month. His total saving from the start of service will be Rs. 11040 after
18 Months
19 Months
20 Months
20 Months
Consider the following statements
P: Suman is brilliant
Q: Suman is rich
R: Suman is honest. The negation of the statement ì Suman is brilliant and dishonest if and only if Suman is richî can be ex- pressed as
~ P ^ (Q ↔ ~ R)
~ (Q ↔ (P ^ ~R)
~ Q ↔ ~ P ^ R
~ Q ↔ ~ P ^ R
If ω(≠1) is a cube root of unity, and (1 + ω)7 = A + Bω.Then (A, B) equals
(0,1)
(1,1)
(1,0)
(1,0)
If the mean deviation about the median of the numbers a, 2a, ....., 50a is 50, then |a| equals
2
3
4
4
Let R be the set of real numbers.
Statement-1 : A = {(x, y) ∈R × R : y - x is an integer} is an equivalence relation on R.
Statement-2 : B = {(x, y) ∈ R × R : x = αy for some rational number α} is an equivalence relation on R.
Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is false.
Statement-1 is true, Statement-2 is false.
Consider 5 independent Bernoulliís trials each with a probability of success p. If the probability of at least one failure is greater than or equal to 31/32, then p lies in the interval
(1/2, 3/4]
(3/4, 11/12]
[0, 1/2]
[0, 1/2]
The value of p and q for which the function f(x) =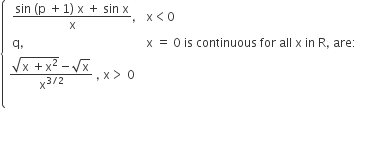
p = 1/2. q = -3/2
p = 5/2, q = 1/2
p = - 3/2, q = 1/2
p = - 3/2, q = 1/2
