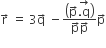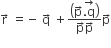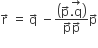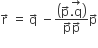Multiple Choice Questions
Multiple Choice QuestionsThe population p(t) at time t of a certain mouse species satisfies the differential equation 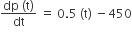 . if p (0) = 850, then the time at which the population becomes zero is
. if p (0) = 850, then the time at which the population becomes zero is
2 log 18
log 9
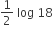
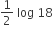
A.
2 log 18
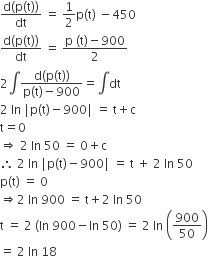
Let a, b ∈ R be such that the function f given by f(x) = ln |x| + bx
2+ ax, x ≠ 0 has extreme values at x = –1 and x = 2.
Statement 1: f has local maximum at x = –1 and at x = 2.
Statement 2: 
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
If: R →R is a function defined by  where [x] denotes the greatest integer function, then f is
where [x] denotes the greatest integer function, then f is
continuous for every real x
discontinous only at x = 0
discontinuous only at non-zero integral values of x
discontinuous only at non-zero integral values of x
Let P and Q be 3 × 3 matrices with P ≠ Q. If P3= Q3 and P2Q = Q2P, then determinant of(P2+ Q2) is equal to
-2
1
0
0
Consider the function f(x) = |x – 2| + |x – 5|, x ∈ R.
Statement 1: f′(4) = 0
Statement 2: f is continuous in [2, 5], differentiable in (2, 5) and f(2) = f(5).
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Let  be two unit vectors. If the vectors
be two unit vectors. If the vectors 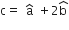 and
and  are perpendicular to each other, then the angle between
are perpendicular to each other, then the angle between  is
is
π/6
π/2
π/3
π/3
Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is
880
629
630
630
Let ABCD be a parallelogram such that  and ∠BAD be an acute angle. If
and ∠BAD be an acute angle. If  is the vector that coincides with the altitude directed from the vertex B the side AD, then
is the vector that coincides with the altitude directed from the vertex B the side AD, then  is given byLet ABCD be a parallelogram such that AB = q,AD = p and ∠BAD be an acute angle. If r is the vector that coincides with the altitude directed from the vertex B to the side AD, then r is given by (1)
is given byLet ABCD be a parallelogram such that AB = q,AD = p and ∠BAD be an acute angle. If r is the vector that coincides with the altitude directed from the vertex B to the side AD, then r is given by (1)