 Multiple Choice Questions
Multiple Choice QuestionsLet A and B be two sets containing 2 elements and 4 elements respectively. The number of subsets of A × B having 3 or more elements is
256
220
219
219
C.
219
Given, n(A) =2, n(B) = B
The number of subsets of AXB having 3 or more elements,
=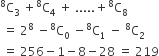
The real number k for which the equation, 2x3 +3x +k = 0 has two distinct real roots in [0,1]
lies between 1 and 2
lies between 2 and 3
lies between -1 and 0
lies between -1 and 0
A ray of light along  get reflected upon reaching X -axis, the equation of the reflected ray is
get reflected upon reaching X -axis, the equation of the reflected ray is
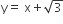
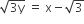


The number of values of k, for which the system of equations
(k+1) x + 8y = 4k
kx + (k+3)y = 3k -1
has no solution, is
infinite
1
2
2
If the equations x2 + 2x + 3 = 0 and ax2 + bx + c = 0, a, b, c ∈ R, have a common root, then a : b : c is
1:2:3
3:2:1
1:3:2
1:3:2
The circle passing through (1,-2) and touching the axis of x at (3,0) also passes through the point
(-5,2)
(2,-5)
(5,-2)
(5,-2)
If x, y, z are in A.P. and tan−1 x, tan−1 y and tan−1 z are also in A.P., then
x= y= z
2x =3y = 6z
6x = 3y= 2z
6x = 3y= 2z
Consider :
Statement − I : (p ∧ ~ q) ∧ (~ p ∧ q) is a fallacy.
Statement − II : (p → q) ↔ (~ q → ~ p) is a tautology.
Statement -I is True; Statement -II is True; Statement-II is a correct explanation for Statement-I
Statement - I is True; Statement -II is true; Statement-II is not a correct explanation for Statement-I
Statement -I is True; Statement -II is False.
Statement -I is True; Statement -II is False.
