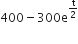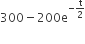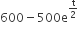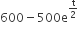Multiple Choice Questions
Multiple Choice QuestionsIf A is a 3x3 non- singular matrix such that AAT = ATA, then BBT is equal to
B-1
B-1
B.
lIf A is non - singular matrix then |A| ≠0
AAT = ATA and B = A-1AT
BBT = (A-1AT)(A-1AT)T
= A-1ATA(A-1)T [∵ (AB)T= BTAT]
=A-1AAT(A-1)T [∵ AAT = ATA]
=AT(A-1)T [ ∵A-1A = l]
=A-1A)T [∵ (AB)T = BTAT]
lT = l
If f and ga re differentiable functions in (0,1) satisfying f(0) =2= g(1), g(0) = 0 and f(1) = 6, then for some c ε] 0,1[
2f'(c) = g'(c)
2f'(c) = 3g'(c)
f'(c) = g'(c)
f'(c) = g'(c)
If fk(x) = 1/k (sink x + cosk x), where x ε R and k ≥1, then f4 (x)-fo (x) equal to
1/6
1/3
1/4
1/4
Let A and B be two events such that 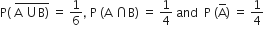 where
where  . Then, the events A and B are
. Then, the events A and B are
independent but not equally likely
independent and equally likely
mutually exclusive and independent
mutually exclusive and independent
If =-1 and x =2 are extreme points of f(x) =α log|x| + βx2 +x, then
α = -6, β = 1/2
α = -6, β = -1/2
α = 2, β = -1/2
α = 2, β = -1/2
Let the population of rabbits surviving at a time t be governed by the differential equation.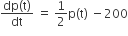 If p(0) = 100 then p(t) is equal to
If p(0) = 100 then p(t) is equal to