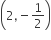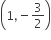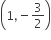Multiple Choice Questions
Multiple Choice QuestionsThe eccentricity of an ellipse whose centre is at the origin is 1/2. If one of its directives is x= –4, then the equation of the normal to it at (1,3/2) is
x + 2y = 4
2y – x = 2
4x – 2y = 1
4x – 2y = 1
C.
4x – 2y = 1
Eccentricity of ellipse =1/2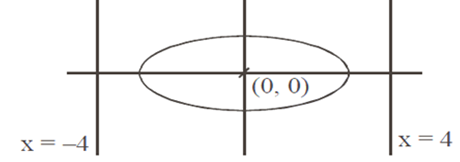
Now, a/e = -4
⇒ a = 4 x (1/2) = 2
therefore, b2 = a2(1-e2)
= a2 (1-(1/4)) = 3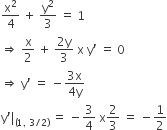
Equation of normal at (1, 3/2)
y-3/2 = 2(x – 1)
⇒ 2y – 3 = 4x – 4
⇒ 4x – 2y = 1
If two different numbers are taken from the set {0, 1, 2, 3, ......., 10), then the probability that their sum, as well as absolute difference, are both multiple of 4, is
7/55
6/55
14/55
14/55
For three events A, B and C,
P(Exactly one of A or B occurs)
= P(Exactly one of B or C occurs)
= P(Exactly one of C or A occurs) = 1/4and P(All the three events occur simultaneously) = 1/16.Then the probability that at least one of the events occurs, is
3/16
7/32
7/16
7/16
Let a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB.If ∠BPC = β , then tanβ is equal to
4/9
6/7
1/4
1/4
If S is the set of distinct values of 'b' for which the following system of linear equations
x + y + z = 1
x + ay + z = 1
ax + by + z = 0
has no solution, then S is
a singleton
an empty set
an infinite set
an infinite set
Let ω be a complex number such that 2ω +1 = z where z = √-3. if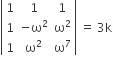
then k is equal to
1
-z
z
z
The radius of a circle, having minimum area, which touches the curve y = 4 – x2 and the lines, y = |x| is
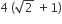
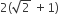
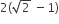
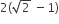
Let k be an integer such that triangle with vertices (k, –3k), (5, k) and (–k, 2) has area 28 sq. units. Then the orthocentre of this triangle is at the point