Multiple Choice QuestionsA particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
x2
ex
x
x
A ball is released from the top of a tower of height h metres. It takes T seconds to reach the ground. What is the position of the ball in T/3 seconds?
h/9 metres from the ground
7h/9 metres from the ground
8h/9 metres from the ground
8h/9 metres from the ground
A projectile can have the same range R for two angles of projection. If T1 and T2 be the time of flights in the two cases, then the product of the two time of flights is directly proportional to
1/R2
1/R
R
R
Which of the following statements is false for a particle moving in a circle with a constant angular speed?
The velocity vector is tangent to the circle.
The acceleration vector is tangent to the circle.
The acceleration vector points to the centre of the circle.
The acceleration vector points to the centre of the circle.
An automobile travelling with speed of 60 km/h, can brake to stop within a distance of 20 cm. If the car is going twice as fast, i.e 120 km/h, the stopping distance will be
20 m
40 m
60 m
60 m
A machine gun fires a bullet of mass 40 g with a velocity 1200 ms−1. The man holding it can exert a maximum force of 144 N on the gun. How many bullets can he fire per second at the most?
one
Four
Two
Two
Two masses m1 = 5 kg and m2 = 4.8 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when lift free to move?
(g = 9.8 m/s2 )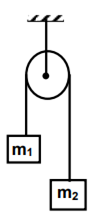
0.2 m/s2
9.8 m/s2
5 m/s2
5 m/s2
A uniform chain of length 2 m is kept on a table such that a length of 60 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg. What is the work done in pulling the entire chain on the table?
7.2 J
3.6 J
120 J
120 J
Switch
then the angle between A and B isπ
