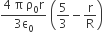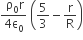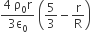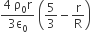Multiple Choice Questions
Multiple Choice QuestionsTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30º with each other. When suspended in a liquid of density 0.8 g cm–3, the angle remains the same. If density of the material of the sphere is 1.6 g cm–3, the dielectric constant of the liquid is
4
3
2
2
C.
2
From FBD of sphere, using Lami theorem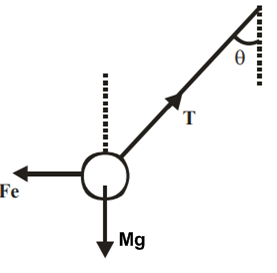
F/Mg = Tan θ .... (i)
when suspended in liquid as θ remains unchanged,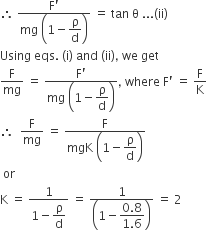
Two conductors have the same resistance a 0°C but their temperature coefficients o resistance are α1 and α2. The respective temperature coefficients of their series parallel combinations are nearly
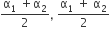
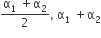
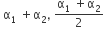
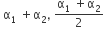
The equation of a wave on a string of linear mass density 0.04 kg m–1 is given by y= 0.02(m) sin 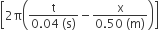 The tension in the string is
The tension in the string is
4.0 N
12.5
0.5 N
0.5 N
Let C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one–fourth its initial value. Then the ratio t1/t2 will be
1
1/2
1/4
1/4
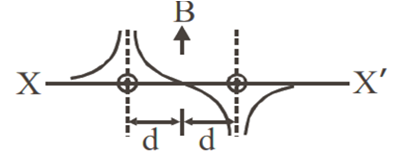
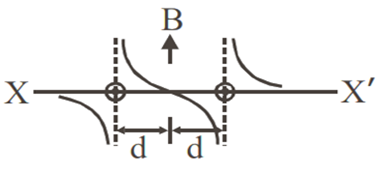
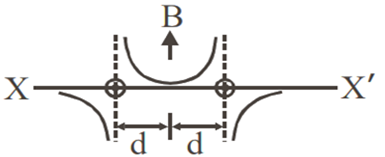
Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper as shown. The variation of the magnetic field B along the line XX' is given by




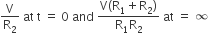
In the circuit shown below, the key K is closed at t = 0. The current through the battery is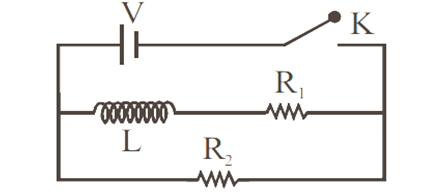



A thin semi–circular ring of radius r has a positive charge q distributed uniformly over it. The net field  at the center O is
at the center O is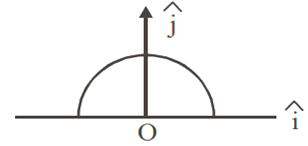

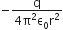
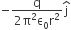
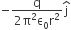
In a series LCR circuit, R = 200 Ω and the voltage and the frequency of the main supply is 220 V and 50 Hz respectively. On taking out the capacitance from the circuit the current lags behind the voltage by 30º. On taking out the inductor from the circuit the current leads the voltage by 30º. The power dissipated in the LCR circuit is
305 W
210 W
zero
zero
Let there be a spherically symmetric charge distribution with charge density varying as 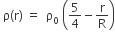 upto r = R, and ρ(r) = 0 for r > R, where r is the distance from the origin. The electric field at a distance r ( r < R) from the origin is given by
upto r = R, and ρ(r) = 0 for r > R, where r is the distance from the origin. The electric field at a distance r ( r < R) from the origin is given by