 Multiple Choice Questions
Multiple Choice QuestionsTwo particles are executing simple harmonic motion of the same amplitude Aand frequency ω along the x - axis. Their mean position is separated by distance X0 (X0 >A). If the maximum separation between them is (X0 + A), the phase difference between their motion is
π/3
π/4
π/6
π/6
A.
π/3
x1 = A sin( ωt + Φ1)
x2 = A sin( ωt + Φ2)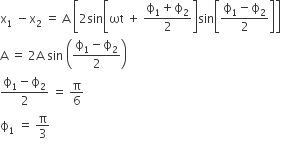
100g of water is heated from 30°C to 50°C ignoring the slight expansion of the water, the change in its internal energy is (specific heat of water is 4184 J/Kg/K)
8.4 kJ
84 kJ
2.1 kJ
2.1 kJ
A thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heat γ.It is moving with speed v and it suddenly brought to rest. Assuming no heat is lost to the surroundings, its temperature increases by
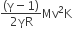
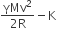
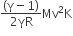
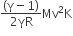
A mass M, attached to a horizontal spring, executes SHM with an amplitude A1. When the mass M passes through its mean position than a smaller mass m is placed over it and both of them move together with amplitude A2. The ratio of (A1/A2) is
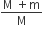
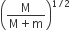
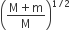
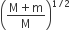
Water is flowing continuously from a tap having an internal diameter 8 × 10-3 m. The water velocity as it leaves the tap is 0.4 ms-1. The diameter of the water stream at a distance 2 × 10-1 m below the tap is close
to:
7.5 x 10-3 m
9.6x 10-3 m
3.6x 10-3 m
3.6x 10-3 m
Three perfect gases at absolute temperature T1, T2 and T3 are mixed. The masses of molecules are m1,m2 and m3 and the number of molecules is n1,n2 and n3 respectively.Assuming no loss of energy, the final temperature of the mixture is
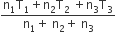
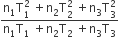
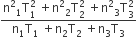
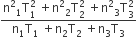
A Carnot engine operating between temperatures T1 and T2 has efficiency 1/6. When T2 is lowered by 62 K, its efficiency increases to 1/3. Then T1 and T2 are, respectively
372 K and 330 K
330 K and 268 K
310 K and 248 K
310 K and 248 K
A boat is moving due east in a region where the earth's magnetic field is 5.0 × 10-5 NA-1m-1 due north and horizontal. The boat carries a vertical aerial 2m long. If the speed of the boat is 1.50 ms-1, the magnitude of the induced emf in the wire of aerial is
0.75 mV
0.50 mV
0.15 mV
0.15 mV
A fully charged capacitor C with initial charge q0 is connected to a coil of self inductance L at t = 0. The time at which the energy is stored equally between the electric and the magnetic fields is
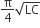



A current I flows in an infinitely long wire with cross-section in the form of a semicircular ring of radius R. The magnitude of the magnetic induction along its axis is




