 Multiple Choice Questions
Multiple Choice QuestionsA spectrometer gives the following reading when used to measure the angle of a prism.
Main scale reading: 58.5 degree
Vernier scale reading: 09 divisions
Given that 1 division on the main scale corresponds to 0.5 degree. Total divisions on the vernier scale is 30 and match with 29 divisions of the main scale. The angle of the prism from the above data
58.59 degree
58.77 degree
58.65 degree
58.65 degree
C.
58.65 degree
A diatomic molecule is made of two masses m1 and m2 which are separated by a distance r. If we calculate its rotational energy by applying Bohr's rule of angular momentum quantization, its energy will be given by (n is an integer)
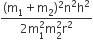
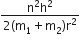
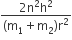
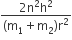
A cylindrical tube, open at both ends, has a fundamental frequency, f, in the air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air-column is now
m1r1:m2r2
m1 :m2
r1 :r2
r1 :r2
This question has statement 1 and statement 2. Of the four choices given after the statements, choose the one that best describes the two statements.
If two springs S1 and S2 of force constants k1 and k2, respectively, are stretched by the same force, it is found that more work is done on spring S1 than on spring S2.
Statement 1: If stretched by the same amount, work done on S1, will be more than that on S2
Statement 2 : k1 < k2
Statement 1 is false, Statement 2 is true
Statement 1 is true, Statement 2 is false
Statement 1 is true, Statement 2 is the correct explanation for statement 1
Statement 1 is true, Statement 2 is the correct explanation for statement 1
A thin liquid film formed between a U-shaped wire and a light slider supports a weight of 1.5 x10–2N (see figure). The length of the slider is 30 cm and its weight negligible. The surface tension of the liquid film is
0.0125 Nm-1
0.1 Nm-1
0.05 Nm-1
0.05 Nm-1
A boy can throw a stone up to a maximum height of 10 m. The maximum horizontal distance that the boy can throw the same stone up to will be
 m
m
10 m
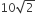 m
m
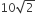 m
m
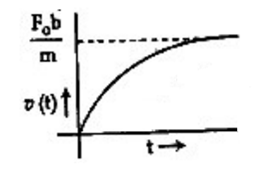
A particle of mass m is at rest at the origin at time t = 0. It is subjected to a force F (t) = F0e–bt in the x direction. Its speed v(t) is depicted by which of the following curves?



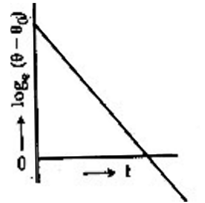
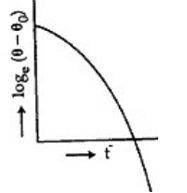
A liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge (θ – θ0) and t is


The mass of a spaceship is 1000 kg. It is to be launched from the earth's surface out into free space. The value of 'g'and 'R'(radius of earth) are 10 m/s2 and 6400km respectively. The required energy for this work will be;
6.4 x1011 J
6.4 x108 J
6.4 x109 J
6.4 x109 J
A Carnot engine, whose efficiency is 40%, takes in heat from a source maintained at a temperature of 500 K It is desired to have an engine of efficiency 60%. Then, the intake temperature for the same exhaust (sink) temperature must be
the efficiency of Carnot engine cannot be made larger than 50%
1200 K
750 K
750 K
