 Multiple Choice Questions
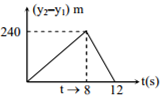
Multiple Choice QuestionsTwo stones are thrown up simultaneously from the edge of a cliff 240 m high with an initial speed of 10 m/s and 40 m/s respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first? (Assume stones do not rebound after hitting the ground and neglect air resistance, take g = 10 m/s2 )
C.

The concept of relative motion can be applied to predict the nature of motion of one particle with respect to the other.
Consider the stones thrown up simultaneously as shown in the diagram below.
Considering the motion of the second particle with respect to the first we have relative acceleration
|a21| = |a2-a1| = g-g = 0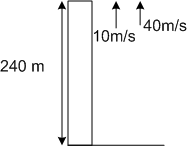
Thus, motion of the first particle is straight line with respect to the second particle till the first particle strikes ground at a time given by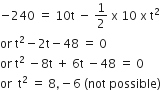
Thus, distance covered by the second particle with respect to the first particle in 8s is
S12 = (v21) t = (40-10)(8s)
= 30 x 8 = 240m
Similarly, time taken by the second particle to strike the ground is given by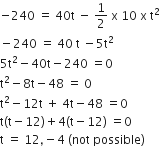
Thus, after the 8s magnitude of relative velocity will increases up to 12 s when the second particle strikes the ground.
Given in the figure are two blocks A and B of weight 20 N and 100 N respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is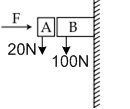
100N
80 N
120 N
150 N
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
44%
50%
56%
62%
From a solid sphere of mass M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is :
h2/4R
3h/4
5h/8
3h2/8R
From a solid sphere of mass M and radius R, a cube of the maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is
![]()
![]()
![]()
![]()
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure. Taking gravitational potential V = 0 at r = ∞, the potential at the centre of the cavity thus formed is (G = gravitational constant)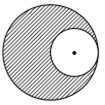
-GM/2R
-GM/R
-2GM/3R
-2GM/R
The period of oscillation of a simple pendulum is ![]() . The measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using wrist watch of 1 s resolution. The accuracy in the determination of g is:
. The measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using wrist watch of 1 s resolution. The accuracy in the determination of g is:
2%
3%
1%
5%
A pendulum made of a uniform wire of cross-sectional area A has time period T. When an additional mass M is added to its Bob, the time period changes TM. If Young's modulus of the material of the wire is Y, then 1/Y is equal to (g = gravitational acceleration)
![]()
![]()
![]()
![]()
Consider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume ![]() and pressure.
and pressure.![]() If the shell now undergoes an adiabatic expansion the relation between T and R is
If the shell now undergoes an adiabatic expansion the relation between T and R is
T ∝ e-R
T ∝ e-3R
T ∝ (1/R)
T ∝(1/R3)
A solid body of constant heat capacity 1 J/°C is being heated by keeping it in contact with reservoirs in two ways:
(i) Sequentially keeping in contact with 2 reservoirs such that each reservoir supplies the same amount of heat.
(ii) Sequentially keeping in contact with 8 reservoirs such that each reservoir supplies the same amount of heat. In both the cases body is brought from an initial temperature 100°C to final temperature 200°C. Entropy change of the body in the two cases respectively is:
ln2,4ln2
ln2,ln2
ln2,2ln2
2ln2,8ln2
