Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
P and Q are the points of trisection of AB,
therefore, AP=PQ=QB
Thus, P divides AB internally in the ratio 1:2 and Q divide AB internally in the ratio 2:1.
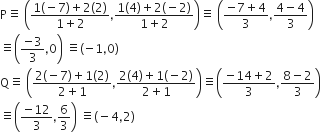
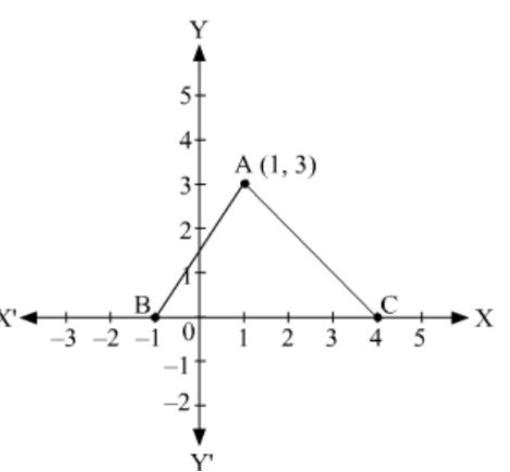
In fig., the area of triangle ABC (in sq. units) is
15
10
7.5
2.5
C.
7.5
From the figure, the coordinates of A, B, and C are (1,3), (-1, 0) and (4, 0)
respectively.
The coordinates of the point P dividing the line segment joining the points A(1, 3) and B(4, 6) in the ratio 2 : 1 are
( 2, 4 )
( 3, 5 )
( 4, 2 )
( 5, 3 )
B.
( 3, 5 )
It is given that the point P divides AB in the ratio 2 : 1.
Using the section formula, the coordinates of the point P are
Hence, the coordinates of the point P are (3,5).
If the coordinates of the one end of a diameter of a circle are (2, 3) and the coordinates of its centre are (-2, 5), then the coordinates of the other end of the diameter are:
( -6, 7)
( -6, -7)
( 6,7)
( -6, -7)
A.
( -6, 7)
Let the coordinates of the other end of the diameter be (x,y).
We know that the centre is the midpoint of the diameter. So, O(-2, 5 )
is the midpoint of the diameter AB. The coordinates of the point A and B are (2,3) and (x,y) respectively.
Using midpoint formula, we have,
Hence, the coordinates of the other end of the diameter are ( -6,7).
If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value (s) of p.
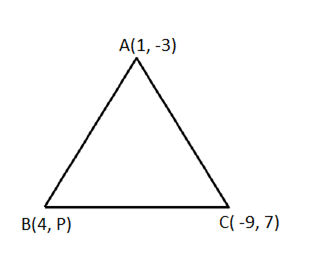
The area of the triangle, whose vertises are (x1, y1), (x2, y2) and (x3, y3) is
[ x1 (y2 - y3) + x2 ( y3 - y1 ) + x3 ( y1 - y2 ) ]
Substituting the given coordinates
=
