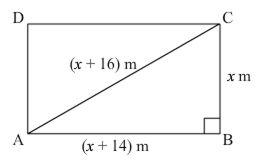
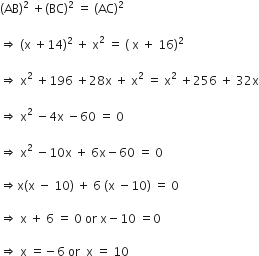Find the values of k so that the area of the triangle with vertices (1,-1), (-4, 2k) and (-k, 5) is 24 sq. units
The vertices of the given ΔABC are A(1 ,-1), B( -4, 2k ) and C (-k, 5)
Area of ΔABC =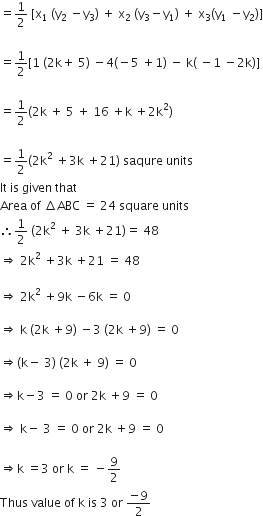
Show that the points (-2, 3), (8, 3) and (6, 7) are the vertices of a right
triangle
If a≠b≠0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear.
Let A(a, a2), B(b, b2) and C(0, 0) be the coordinates of the given points.
We know that the area of a triangle having vertices (x1, y1), (x2, y2) and (x3, y3) is ∣∣12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]∣∣ square units.
So,
Area of ∆ABC\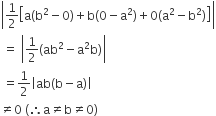
Since the area of the triangle formed by the points (a, a2), (b, b2) and (0, 0) is not zero, so the given points are not collinear.