Find all zeroes of the polynomial (2x⁴ - 9x³ + 5x² + 3x-1) if two of its zeroes are ( 2 + √3 ) and ( 2 - √3 ).

It is given that ( 2 + √3 ) and ( 2 - √3 ) are two zeros of 2x⁴ - 9x³ + 5x² + 3x-1

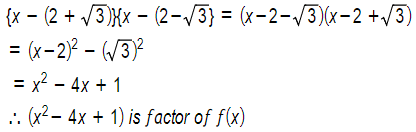
Let us now divide f(x) by x²-4x + 1

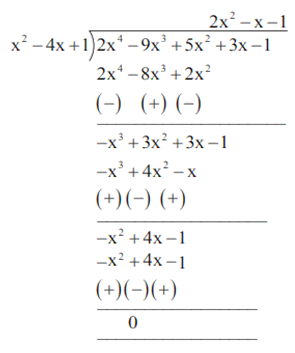
therefore, we have,

 f(x) = (x²- 4x + 1)(2x²-x-1)

Hence, other two zeros of f(x) are the zeros of the polynomial 2x²-x-1

We have, 

2x²-x-1 = 2x²- 2x+ x-1

= 2x (x-1) + 1(x-1)

= (2x+ 1)(x-1)

Hence, the other two zeros are - 1/2 and 1.