Book Store

Download books and chapters from book store.
Currently only available for.
CBSE Gujarat Board Haryana Board

Previous Year Papers

Download the PDF Question Papers Free for off line practice and view the Solutions online.
Currently only available for.
Class 10 Class 12

A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (π = 22/7)

Let the radius of the conical vessel = r₁ = 5 cm
Height of the conical vessel = h₁ = 24 cm
Radius of the cylindrical vessel = r₂
Let the water rise upto the height of h₂ cm in the cylindrical vessel.
Now, volume of water in conical vessel = volume of water in cylindrical vessel
$therefore space 1 third straight pi subscript 1 straight r squared straight h subscript 1 space equals space straight pi subscript 2 straight r squared straight h subscript 2 therefore space straight r subscript 1 superscript 2 straight h space equals 3 straight r subscript 2 superscript 2 straight h subscript 2 superscript space therefore space 5 space straight x space 5 space straight x space 24 space equals space 3 space straight x space 10 space straight x space 10 space straight x space straight h subscript 2 therefore straight h subscript 2 space equals space fraction numerator 5 straight x space 5 straight x 24 over denominator 3 straight x 10 space straight x 10 end fraction space equals 2 space cm Thus comma space the space water space will space rise space upto space the space height space of space 2 space cm space in space the space cylinderical space vessel.$

6476 Views

In Fig., a tent is in the shape of a cylinder surmounted by a conical top of the same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre. (use π = 22/7)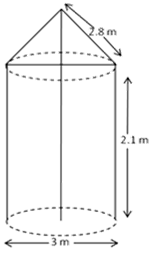

In the given figure,

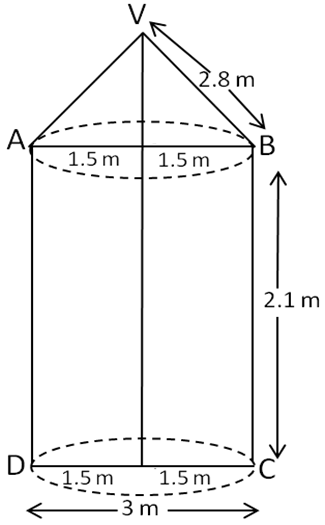Given diameter 3m
For conical portion,
radius = 3/2 = 1.5m and length is 2.8m
∴ S₁ = curved surface area of conical portion
∴ S₁ = πrl
= π x 1.5 x 2.1
= 6.3π m²
Area of canvas used for making tent = S₁+S₂
=4.2π +6.3π
= 10.5π
=10.5 x (22/7)
=33m²
Thus, total cost of the canvas at the rate of Rs. 500 per m² = 500 x 33 =16500
Rs. 16500 is total cost.

4302 Views

A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 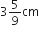$3 5 over 9 cm$ . Find the diameter of the cylindrical vessel.

Given,
Diameter of sphere 12 cm,
therefore radius of sphere is 12/2 = 6 cm

$Volume space of space sphere space equals 4 over 3 πr cubed space equals space 4 over 3 straight pi space straight x left parenthesis 6 right parenthesis cubed space equals space 288 straight pi space cm squared Let space straight R space be space the space radius space of space cylindrical space vessel. Reise space in space the space water space level space of space cylindrical space equals straight h equals 3 5 over 9 space cm space equals 312 over 9 space cm Increase space in space volume space of space cylindrical space vessel space equals πR squared straight h space equals πR squared space straight x 32 over 9 space equals 32 over 9 πR squared Now comma space volume space of space water space displaced space by space the space sphere space is space equal space to space volume space of space sphere therefore comma space 32 over 9 πR squared space equals 288 straight pi straight R squared equals fraction numerator 288 space straight x 9 over denominator 32 end fraction space equals 81 straight R equals 9 space cm Diameter space of space the space cylindrical space vessel space equals 2 space straight x space straight R space equals 2 space straight x space 9 equals 18 space cm$

2477 Views

A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.

$[Use π = \frac{22}{7}]$

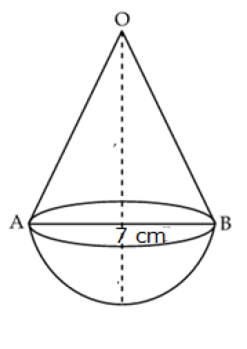
Radius of hemi-sphere = 7 cm.

Radius of cone 7 cm.

Height of cone = diameter = 14 cm.

Volume of solid = Volume of cone + Volume of hemi-sphere

$= \frac{1}{3} {πr}^{2} h + \frac{2}{3} {πr}^{3} = \frac{1}{3} {πr}^{2} (h + 2 r) = \frac{1}{3} x \frac{22}{7} x 7 x 7 (14 + 2 x 7) = \frac{1}{3} x \frac{22}{7} x 7 x 7 x 28 = \frac{22 x 7 x 7 x 28}{3 x 7} = \frac{4312}{3} {cm}^{3}$

If the radius of the base of a right circular cylinder is halved, keeping the height the same, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is

1 : 2
2 : 1
1 : 4
4 : 1

1 : 4

Let the original radius and the height of the cylinder be r and h respectively.

$V o l u m e o f t h e o r i g i n a l c y l i n d e r = {πr}^{2} h Radius of the new cylinder = \frac{r}{2} Height of the new cylinder = h Volume of the new cylinder = π {(\frac{r}{2})}^{2} h = \frac{{πr}^{2} h}{4} Required ratio = \frac{Volume of the new cylinder}{Volume of the original cylinder} = \frac{\frac{{πr}^{2} h}{4}}{{πr}^{2} h} = \frac{1}{4} = 1 : 4$

Chapter Chosen

Book Chosen

Subject Chosen

Book Store

Previous Year Papers

Surface Areas and Volumes