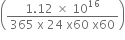Io, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is 4.22 Ă— 108Â m. Show that the mass of Jupiter is about one-thousandth that of the sun.
Orbital period of I0 , TI0 = 1.769 daysÂ
                   = 1.769 × 24 × 60 × 60 sÂ
Orbital radius of I0 , RI0 = 4.22 × 108 mÂ
Satellite I0Â is revolving around the JupiterÂ
Mass of the Jupiter is given by,Â
MJÂ = 4Ï€2RI03Â / GTI02Â Â Â Â Â Â Â Â Â Â Â Â Â ...(i)Â
where,Â
MJÂ = Mass of Jupiter,Â
G = Universal gravitational constant,
Orbital period of the earth,
Te = 365.25 days
  = 365.25 × 24 × 60 × 60 sÂ
Orbital radius of the Earth,
Re = 1 AU = 1.496 × 1011 mÂ
Mass of sun is given as,Â
Ms = 4Ï€2Re3 / GTe2               ...(ii)Â
Therefore,
Ms /Â
MJÂ =Â
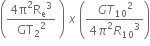
       = Â
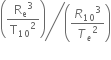
Substituting the values,Â
=
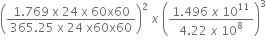
 = 1045.04
∴ Ms / MJ  ~ 1000Â
      Ms ~ 1000 × MJÂ
Hence, it can be inferred that the mass of Jupiter is about one-thousandth that of the Sun.
232 Views

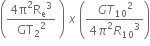
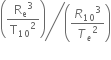
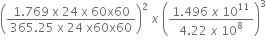
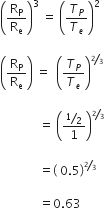 Â
 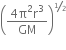 Â
 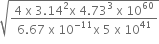 Â
 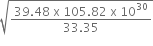
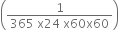 yearsÂ
years