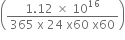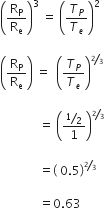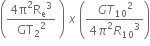
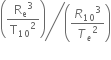
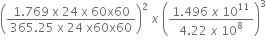
Does the escape speed of a body from the earth depend on
(a) the mass of the body,
(b) the location from where it is projected,
(c) the direction of projection,
(d) the height of the location from where the body is launched?

Does the escape speed of a body from the earth depend on:
(a) the mass of the body,
(b) the location from where it is projected,
(c) the direction of projection,
(d) the height of the location from where the body is launched?
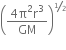
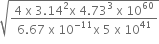
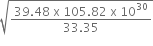
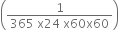 years
years