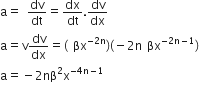A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration, if the kinetic energy of the particle becomes equal to 8 x 10-4 J by the end of the second revolution after the beginning of the motion?
0.15 m/s2
0.18 m/s2
0.2 m/s2
0.2 m/s2
D.
0.2 m/s2
Given, mass of particle. m = 0.01 kg
Radius of circle along which particle is moving , r = 6.4 cm
Kinetic energy of particle, K.E. = 8 x 10-4 J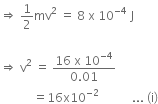
Given that, KE of particle is equal to 8 x 10-4 J by the end of second revolution after the beginning of the motion of particle.
It means, initial velocity (u) is 0 m/s at this moment.
Now, using the Newton's 3rd equation of motion,
v2 = u2 + 2as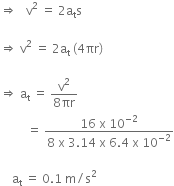
If the velocity of a particle is v = At + Bt2, where A and B are constants, then the distance travelled by it between 1 s and 2 s is,
3A + 7B
![]()
![]()
![]()
B.
![]()
Velocity of the particles is given as,
v = At + Bt2, where a and B are constants.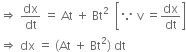
Integrating both sides, we get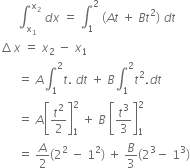
Therefore, distance travelled between 1 s and 2 s is,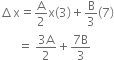
A particle moves so that its position vector is given by r = cos ![]() where
where ![]() is a constant. Which of the following is true?
is a constant. Which of the following is true?
velocity and acceleration both are parallel to r
velocity is perpendicular to r and acceleration is directed towards the origin
velocity is perpendicular to r and acceleration is directed away from the origin
velocity and acceleration both are perpendicular to r
B.
velocity is perpendicular to r and acceleration is directed towards the origin
Position vector of the article is given by,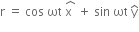
where  is a constant.
is a constant.
Velocity of the particle is,
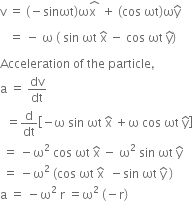
The particle is at a point P. That is, its position vector is directed as shown below:
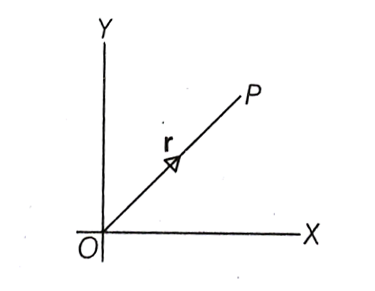 Therefore, acceleration is directed towards -r, that is towards "O"
Therefore, acceleration is directed towards -r, that is towards "O"
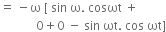
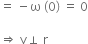
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?




C.

The question is illustrated in the figure below,
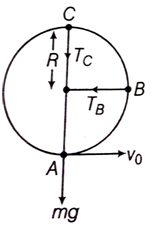 Let, the tension at point A be TA.
Let, the tension at point A be TA.
Using Newton's second law, we have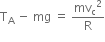
Energy at point A = 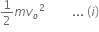
Energy at point C is,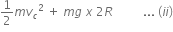
At point C, using Newton's second law,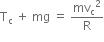
In order to complete a loop, Tc 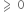
So,
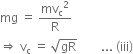
From equation (i) and (ii)
Using the principle of conservation of energy,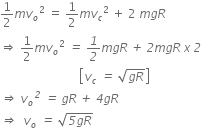
A particle of unit mass undergoes one-dimensional motion such that its velocity according to
V(x) = βx-2n where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x is given by
-2nβ2 x-2n-1
-2nβ2 x-4n-1
-2β x-2n+1
-2β x-2n+1
B.
-2nβ2 x-4n-1
Given, v = βx-2n