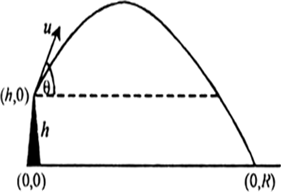

A particle is projected with velocity ![]() at such an angle that it just clears two walls of equal height h which are at a distance 2h from each other. Show that time of passing between the two walls is
at such an angle that it just clears two walls of equal height h which are at a distance 2h from each other. Show that time of passing between the two walls is ![]()


The situation is as shown in figure. Let w.r.t. A (point of fire of first shot), the position of bird is ![]()
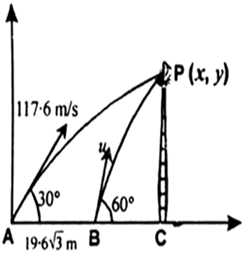
Position of first shot at any instant:
As both the shots hit the bird simultaneously, therefore at the instant of hitting positions of both the shots will be same.
i.e. ![]()
From condition ![]() we get
we get
A stone is projected with velocity (√2gh) from the top of building h meter high. Show that it will fall farthest at a distance (2√2)h.


Let the body be projected with velocity u making an angle θ with the horizontal.
The direction of motion of body after t seconds of throw is given by the equation,
![]()
Here at time, t = 3 the value of ![]() is
is ![]() and at t = 5s the value of
and at t = 5s the value of ![]() is
is ![]()
∴ ![]() ...(1)
...(1)
and
![]() ...(2)
...(2)
From (2),
![]() ...(3)
...(3)
Substituting ![]() in equation (1), we get
in equation (1), we get
![]() ...(4)
...(4)
The horizontal range of the body,
![]()
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/PHEN11039744-11.png)
Therefore, the body falls at a distance of 200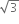 from the point of projection.
from the point of projection.
