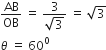The position x of a particle with respect to time t along x- axis is given by x = 9t2 -t3 where x is in meter and t in second. What will be the position of this particle when it achieves maximum speed along the +x direction?
32 m
54 m
81 m
81 m
B.
54 m
At the instant when speed is maximum, its acceleration is zero.
Given, the position x of particle with respect to time t along x- axis
x = 9t2-t3 ... (i)
differentiating Eq. (i) with respect to time, we get speed, ie, 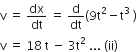
Again differentiating Eq. (ii) with respect to time, we get acceleration, ie, 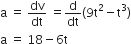
Now, when speed of particle is maximum, its acceleration is zero, ie,
a= 0
18-6t = 0 or t = 3s
Putting in eq (i) We, obtain the position of a particle at that time.
x = 9 (3)2 - (3)3 = 9 (9) -27
= 81-27 = 54 m
A particle of mass is projected with the velocity v making an angle of 45o with the horizontal.
When the particle lands on the level ground the magnitude of the change in its momentum will be
2 mv
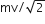


C.


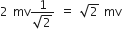
A particle shows distance -time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point
B
C
D
D
A.
B
The particle has maximum instantaneous velocity at that point at which its slope is maximum.
Therefore, vmax = dx/dt = maximum slope
From the figure, it is obvious that at point C, the slope is maximum, hence at this point velocity is maximum.
A particle moves in a straight line with a constant acceleration. It changes its velocity from 10 ms-1 to 20 ms-1 while passing through a distance 135 m in t second. The value of t is
10
1.8
12
12
D.
12
The problem requires kinematics equations of motion
Let u and v be the first and final velocities of particle an a and s be the constant acceleration and distance covered by it.
From third equation of motion
v2 = u2 + 2as
(20)2 = (10)2 + 2a x 135
or
a = 300/2 x135 = 10/9 ms-2
Now using first equation of motion,
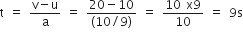
A particle starting from the origin (0,0) moves in a straight line in the (x,y) plane. Its coordinates at a later time are (  ). The path of the particle makes with the x -axis an angle of:
). The path of the particle makes with the x -axis an angle of:
30o
45o C
60o C
60o C
C.
60o C
The slope of the path of the particle gives the measure of angle required.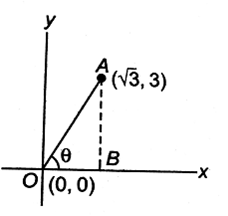
Draw the situation as shown. OA represents the path of the particle starting from origin O (0,0). Draw a perpendicular from point A to X- axis. Let path pf the particle makes and angle θ with the x -axis, then
tan θ = slope of line OA