Define the following:
(i) Equal vector (ii) Negative vector
(iii) Parallel vector (iv) Co-planer vector
(v) Co-initial vector (vi) Co-linear vector
(i) Equal vector: Two vectors are said to be equal vectors, if they have equal magnitude and same direction. Figure (i) shows the two vectors  having same magnitude and same direction, therefore, they are equal vectors.
having same magnitude and same direction, therefore, they are equal vectors.
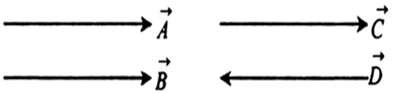
(ii) Negative vector: A vector is said to be negative of another vector if they have same magnitude and opposite direction. Figure (ii) shows the two vectors  having same magnitude and opposite direction, therefore, they are negative of each other.
having same magnitude and opposite direction, therefore, they are negative of each other.
(iii) Parallel vector: Two vectors are said to be parallel if the lines of their action are either same or parallel. The magnitude of two vectors need not to be equal. The parallel vectors are of two types:
(a) Like parallel vector: Two vectors are said to be like parallel vectors if they have same direction.
(b) Unlike parallel vectors: Two vectors having opposite direction are called unlike parallel vectors.
(iv) Co-planer vectors: The vectors lying in one plane are called co-planer vectors.
(v) Co-initial vectors: The vectors having common initial point are called co-initial vectors.
(vi) Co-linear vectors: The vectors having same line of action are called co-linear vectors.
705 Views