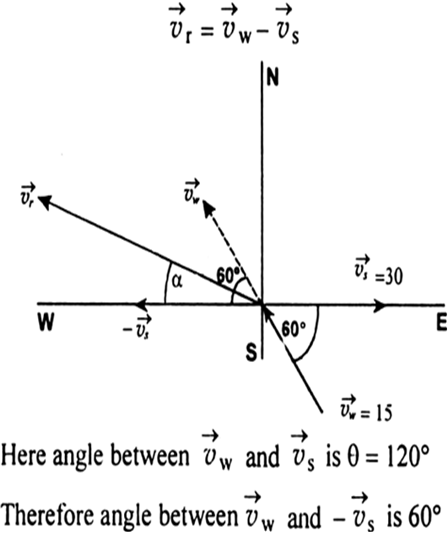

Let ![]() be the velocities of particles A and B respectively. The relative velocity of B relative to A will be
be the velocities of particles A and B respectively. The relative velocity of B relative to A will be ![]() To find
To find ![]() we will first change
we will first change ![]() into
into ![]() and then add to
and then add to ![]() as shown in figure. As
as shown in figure. As ![]() makes an angle of
makes an angle of ![]() with
with ![]() therefore
therefore ![]() will subtend an angle
will subtend an angle ![]() with
with ![]()
Now, ![]()
![]()
or ![]()
![]()
or ![]()
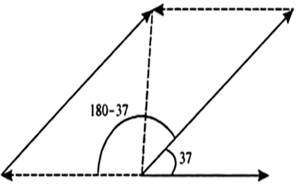
The angle that the relative velocity makes with ![]() is,
is,
![]()
![]()
or ![]()
Here,
Velocity of train A, 
Velocity of train B, ![]()
Acceleration of train A, ![]()
Acceleration of train B, ![]()
Let initially A be ahead of B by a distance d. Let SB and SA be the distances travelled by trains B and A respectively in 50s.
As at t = 50 s the position of both the trains is same.
Therefore,
![]()
Now,
![]()
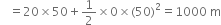
![]()
![]()
∴ original distance between them is, 
![]()
Two cars A and B are travelling in same direction with speed ![]() respectively
respectively ![]() When car A is d distance behind the car B, the brakes on A are applied, causing retardation
When car A is d distance behind the car B, the brakes on A are applied, causing retardation ![]() Show that to prevent a collision between A and B it is necessary that
Show that to prevent a collision between A and B it is necessary that
![]()