
Volume - scalar quantity
Speed - scalar quantity
Acceleration - vector quantity
Density - scalar quantity
Number of moles - scalar quantity
Velocity - vector quantity
Angular frequency - scalar quantity
Angular velocity - vector quantity
(a)True, because magnitude is a pure number.
(b) False, each component of a vector is always a vector, not a scalar.
(c) False, total path length can also be more than the magnitude of displacement vector of a particle. e.g. when a particle follows the arc of circle, the length of path is greater than magnitude of the displacement.
This statement is true only if the particle is moving in a straight line.
(d) True, because the total path length is either greater than or equal to the magnitude of the displacement vector.
(e) True, as the three vectors cannot be represented by the three sides of a triangle taken in the same order.
State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(a) adding any two scalars,
(b) adding a scalar to a vector of the same dimensions,
(c) multiplying any vector by any scalar,
(d) multiplying any two scalars,
(e) adding any two vectors,
(f) adding a component of a vector to the same vector.
(a) If the scalars are similar type of quantities, adding of scalars will be meaningful. Scalars of the same dimension can only be added.
(b) Adding a scalar to a vector of the same dimension is meaningless. a scalar cannot be added to a vector.
(c) Any vector can be multiplied by a scalar. A vector when multiplied by a scalar quantity will give us a vector quantity. When the vector quantity acceleration is multiplied by m, we get a force, 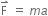 , which is a meaningful operation.
, which is a meaningful operation.
(d) Two scalars can be multiplied together. For example, when power is multiplied by time t, we get the quatity, work done.
(e) Adding any two vectors is meanigless because two vectors of the same dimnsion can be added.
(f) Adding a component of a vector to the same vector is meaningful. Because both the vectors are of the same dimensions.
