
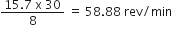
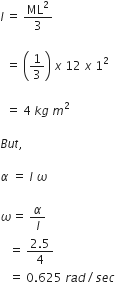
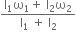
 I1ω12
I1ω12  I2ω22
I2ω22  ( I1ω12 + I2ω22)
( I1ω12 + I2ω22)  ( I1 + I2) ω2
( I1 + I2) ω2 ( I1 + I2)
( I1 + I2) 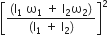

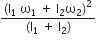
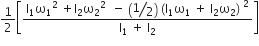
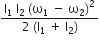
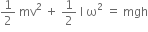
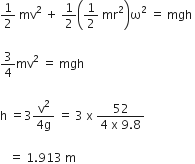


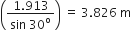
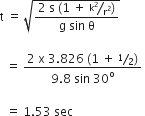
(Hint: Consider the equilibrium of each side of the ladder separately.)
The given question is illustrated in the figure below: 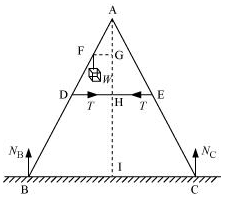
NB = Force exerted on the ladder by the floor point B
NC = Force exerted on the ladder by the floor point C
T = Tension in the rope
BA = CA = 1.6 m
DE = 0. 5 m
BF = 1.2 m
Mass of the weight, m = 40 kg
Draw a perpendicular from A on the floor BC. This intersects DE at mid-point H.
ΔABI and ΔAIC are similar triangles.
∴ BI = IC
Hence, I is the mid-point of BC.
DE || BC
BC = 2 × DE = 1 m
AF = BA – BF = 0.4 m … (i)
D is the mid-point of AB.
Hence, we can write,
AD = ![]() × BA = 0.8 m ...(ii)
× BA = 0.8 m ...(ii)
Using equations (i) and (ii), we get
FE = 0.4 m
Hence, F is the mid-point of AD.
FG||DH and F is the mid-point of AD.
Hence, G will also be the mid-point of AH.
ΔAFG and ΔADH are similar
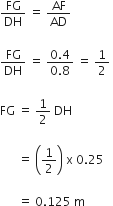
In ΔADH,
AH = (AD2 - DH2)1/2
= (0.82 - 0.252)1/2
= 0.76 m
For translational equilibrium of the ladder, the upward force should be equal to the downward force.
Nc + NB = mg = 392 … (iii)
For rotational equilibrium of the ladder, the net moment about A is
-NB × BI + mg × FG + NC × CI + T × AG - T × AG = 0
-NB × 0.5 + 40 × 9.8 × 0.125 + NC × 0.5 = 0
(NC - NB) × 0.5 = 49
NC - NB = 98 ...(iv)
Adding equations (iii) and (iv), we get
NC = 245 N
NB = 147 N
For rotational equilibrium of the side AB, consider the moment about A,
-NB × BI + mg × FG + T × AG = 0
-245 × 0.5 + 40 X 9.8 × 0.125 + T × 0.76 = 0
∴ T = 96.7 N.
T is the required tension in the rope.
