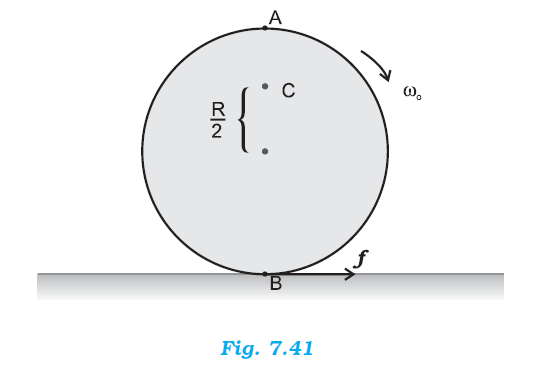
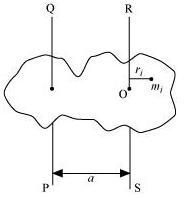
Explain why friction is necessary to make the disc in Fig. 7.41 roll in the direction indicated.
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
A torque is required to roll the given disc. According to the definition of torque, the rotating force should be tangential to the disc. Since the frictional force at point B is along the tangential force at point A, a frictional force is required for making the disc roll.
(a) Force of friction acts opposite to the direction of velocity at point B. The direction of linear velocity at point B is tangentially leftward. Hence, frictional force will act tangentially rightward. The sense of frictional torque before the start of perfect rolling is perpendicular to the plane of the disc in the outward direction.
(b) Frictional force acts opposite to the direction of velocity at point B. Therefore, perfect rolling will begin when the velocity at that point becomes equal to zero. This will make the frictional force acting on the disc zero.
122 Views