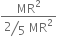A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
Mass of the cylinder, m = 20 kg
Angular speed, ω = 100 rad s–1
Radius of the cylinder, r = 0.25 m
The moment of inertia of the solid cylinder,
I = mr2 / 2
= (1/2) × 20 × (0.25)2
= 0.625 kg m2
∴ Kinetic energy = (1/2) I ω2
= (1/2) × 6.25 × (100)2
= 3125 J
Therefore,
Angular momentum, L = Iω
= 6.25 × 100
= 62.5 Js
That is, there is a magnitude of 62.5 Js angular momentum of the cylinder about it's axis.
182 Views

 I1
I1 ω1
ω1 
 =
= I2 ω22 /
I2 ω22 /  I1 ω12
I1 ω12  I1 (100)2 / I1 (40)2
I1 (100)2 / I1 (40)2  mr2
mr2  =
=  =
=