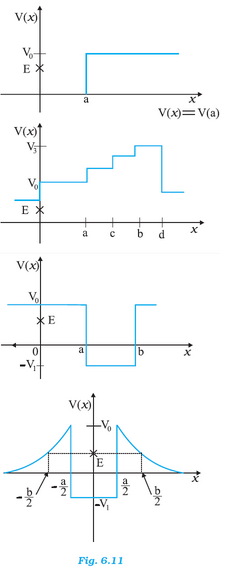
Total energy of a system is,
Energy
= P.E. + K. E.
∴ K.E. = E – P.E
The Kinetic energy of a body is a positive quantity.
It cannot be negative.
Therefore, the particle will not exist in a region where K.E. becomes negative.
(i) For x > a, P.E. (V0) > E
Therefore,
K.E. becomes negative.
Hence, the object cannot exist in the region x > a.
(ii) For x < a and x > b, P.E. (V0) > E.
Therefore,
Kinetic Energy becomes negative.
Hence the object cannot be present in the region x < a and x > b.
iii) x > a and x < b < –V1
In the given case, the condition regarding the positivity of K.E. is satisfied only in the region between
x >
a and
x <
b.
The minimum P.E in this case is –
V1.
Therfore, K.E. =
E – (–
V1) =
E +
V1.
Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than –
V1.
So, the minimum total energy the particle must have is –
V1.
iv) -b/2 < x < a/2 ; a/2 < x < b/2 ; -V1
In the given case, the potential energy (
V0) of the particle becomes greater than the total energy (
E) for -
b/2 < x <
b/2 and -
a/2 <
x <
a/2.
Therefore, the particle will not exist in these regions.
The minimum potential energy in this case is –
V1.
Therefore, K.E. =
E – (–
V1) =
E +
V1.
Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than –
V1.
So, the minimum total energy the particle must have is –
V1.