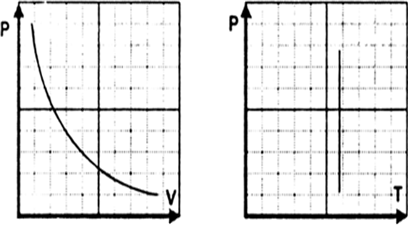
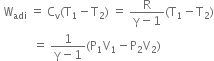What is the equation of state for isothermal process? Plot P versus V graph and P versus T graph for isothermal process for an ideal gas. Discuss the isothermal process using first law of thermodynamics.
An ideal gas equation is,
PV = nRT
Since in isothermal process, T is constant, therefore the equation of state for isothermal process reduces to
PV = constant
P versus V graph and P versus T graph for isothermal process is as shown below.
According to first law of thermodynamics,

178 Views