Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Consider a long thin wire of uniform linear charge density, .
To find: Formula for electric field due to this wire at any point P at a perpendicular distance PC = r from the wire.
Consider a small element of length dx of the wire with centre O, such that OC = x.
Charge on the element, q =
So, electric intensity at P due to the element is given by,
Now, can be resolved into two rectangular components, that is in a perpendicular direction and in a parallel direction.
The parallel component will be cancelled by the parallel component of the field due to charge on a similar element dx of wire on the other half.
The radial components get added.
Therefore,
Effective component of electric intensity due to the charge element,
...(1)
From
From equation (1), we have
Since the wire has infinite length, it’s ends A and B are infinite distances apart.
Therefore, varies from
So, Electric Intensity at P due to the whole wire is given by,
, is the required electric field intensity.
(a) An electric dipole of dipole moment p⃗ consists of point charges +q and –q separated by a distance 2a apart. Deduce the expression for the electric field E⃗ due to the dipole at a distance x from the center of the dipole on its axial line in terms of the dipole moment p⃗. Hence show that in the limit x >> a, E⃗ → 2 p⃗/ (4p ε0 x3).
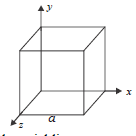
(b) Given the electric field in the region E⃗ = 2x i, find the net electric flux through the cube and the charge enclosed by it.
Electric field on axial line of an electric dipole is given by, 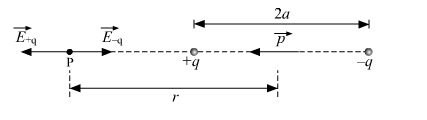
Suppose, P is a point at distance r from the center of the dipole on the side of charge –q.
Electric field at P due to –q is given by, ![]() is the unit vector along the dipole axis.
is the unit vector along the dipole axis.
Electric field at P due to +q is given by,![]()
Therefore, total electric field at point P is,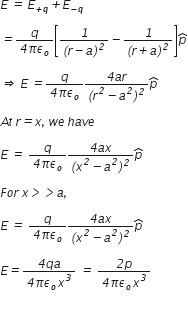
b) Since, the electric field is parallel to the faces parallel to xy and xz planes, the electric flux through them is zero.
Electric flux through the left face,
![]()
(a) Define electric flux. Write its S.I. units.
(b) Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged?a) Electric flux is defined as the total number of electric field lines passing through an area normal to them.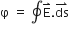
SI unit is Nm2/C.
b) Gauss’s theorem states that the total electric flux through a closed surface is equal to times the net charge enclosed by the surface. 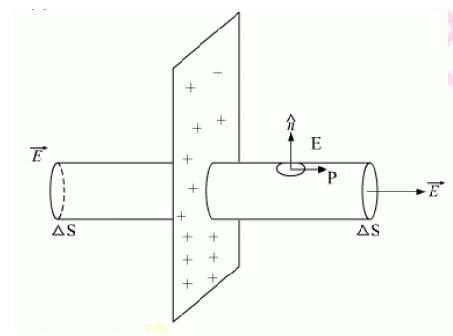
Consider a uniformly charged infinite plane sheet of charge density  .
.
Consider a Gaussian surface inside as shown in the figure which is in the form of a cylinder.
On applying Gauss’s law, we have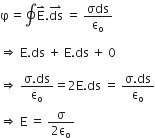
Thus, electric field strength due to an infinite flat sheet of charge is independent of the distance of the point and is directed normally away from the charge.
If the surface charge density s is negative the electric field is directed towards the surface charge.
c) i) Away from the charged sheet.
ii) towards the plane sheet.
Given,
An electron is projected with velocity vx= 2.0.
Distance between the plates = 0.5 cm
Electric field between plates - =
Acceleration,
Using formula
We get,
Simplifying for value of t, we get
The electron covers a vertical distance which is given by
Using Gauss’ laws deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R. (r being the distance from the centre of the shell).
i) Consider a uniformly charged thin spherical shell of radius R carrying charge Q. To find the electric field outside the shell, we consider a spherical Gaussian surface of radius (r >R), concentric with given shell. If E is electric field outside the shell, then by symmetry electric field strength has same magnitude E0 on the Gaussian surface and is directed radially outward.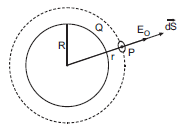
So, electric flux through Gaussian surface is given by, ![]()
Therefore, ![]()
Charge enclosed by the Gaussian surface is Q.
Therefore, using gauss’s theorem, we have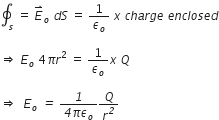
Thus, electric field outside a charged thin spherical shell is the same as if the whole charge Q is concentrated at the centre.
ii) Electric field inside the shell: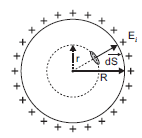
The charge resides on the surface of a conductor. Thus, a hollow charged conductor is equivalent to a charged spherical shell. Let’s consider a spherical Gaussian surface of radius (r < R). If E is the electric field inside the shell, then by symmetry electric field strength has the same magnitude Ei on the Gaussian surface and is directed radially outward.
Electric flux through the Gaussian surface is given by, ![]()
= ![]()
Now, Gaussian surface is inside the given charged shell, so charge enclosed by Gaussian surface is zero.
Therefore, using Gauss’s theorem, we have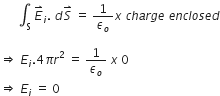
Thus, electric field at each point inside a charged thin spherical shell is zero.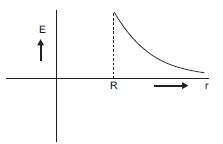
The graph above shows the variation of electric field as a function of R.
