Let, the drift velocities of the wires be vd and vd' respectively.
Area of cross- section of two wires be A and A'.
Then,
A : A' = 1:2
This implies,
A' = 2A
i) When the two wires are connected in series, the same amount of current flows through both the wires.
Implies,
n A vd e = n A' vd' e
where,
n is the number of electrons per unit volume and,
e is the charge on electron.
Therefore,
ii) When the two wires are connected in parallel, the potential difference across the two wires would be the same.
Then,
where, is the resistivity of the two wires.
Therefore,
Resistivity is defined as the measure of resistance to electrical conduction for a given size of material.
For a particular material at specified temperature, resistivity is the electrical resistance per unit length and per unit of cross sectional area.
Resistivity is the inverse of conductivity.
The resistivity of a material depends upon the material and temperature of the material and is independent of the length and area of cross-section.
i) In the absence of electric field the path of electrons are straight lines between successive collisions.
ii) When an electric field is set up from positive to negative charge, the electrons are accelerated towards the negative charge. Therefore, in the presence of electric field the electrons follow a curved path in between successive collisions.
Consider a conductor of length'l' and of uniform area of cross section 'A'. 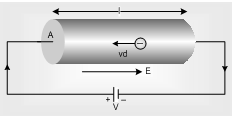
Therefore,
Volume of conductor, V = Al
If, n is the number density of electrons, then
Total number of free electrons in the conductor = Aln
If, e is the total charge on each electron then,
Total charge on electrons in the conductor, q = Alne
Let, a constant potential difference 'V' be applied across the ends of a conductor. Then,
Electric field set up across the conductor, E = V/l
Because of this field, the free electrons present in the conductor begin to move with a drift velocity, vd towards the left hand side.
Therefore,
Time taken by the free electrons to cross the conductor, t = I /Vd
Hence, current, I =
where n is the number of electrons per unit volume.
Given,
Length of the potentiometer wire = l
Internal resistance of the wire = r
Emf of the driving cell =E
External resistance of the cell = R
Current drawn by the wire, I=
Now, using Ohm's law V =IR
i.e, V =
Now, potential gradient of the wire is given by
k = V/l
=
A potentiometer being a null device, does not draw current from the balance point at the balance point. Therefore, potentiometer measures the actual emf of the cell. Whereas, a voltmeter always draws current from the cell and measures the terminal voltage of the cell instead of the actual emf of the cell .
