Two charges + q and -q are placed at a distance a in a uniform electric field. The dipole moment of the combination is , where, θ is the angle between the direction of the field and the line joining the two charges. Which of the following statement(s) is/are correct ?
The torque exerted by the field on the dipole vanishes
The net force on the dipole vanishes
The torque is independent of the choice of coordinates
The net force is independent of a
B.
The net force on the dipole vanishes
C.
The torque is independent of the choice of coordinates
D.
The net force is independent of a
The situation can be diagrammatically as,
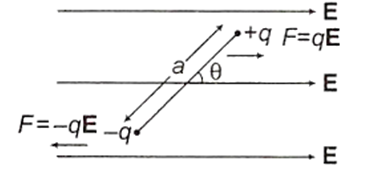
The dipole moment,
The net force on the dipole is always zero while net torque on the dipole is not zero.
Two charges of magnitudes – 2Q and + Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
Using gauss law, we have![]()
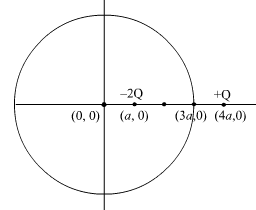
Electric flux is given by, ![]()
A charge q is placed at one corner of a cube. The electric flux through any of the three faces adjacent to the charge is zero. The flux through any one of the other three faces is
q/3ε0
q/6ε0
q/12ε0
q/24ε0
D.
q/24ε0
Consider the diagram

In above the flux coverage of three face is shown in figure which is like a quadrant in any plane. So, flux will be
Given, a cube encloses an electric dipole.
So, the total charge enclosed by the cube is zero.
That is, Q= 0.
Now, using the formula for electric flux as per Gauss’s law of electrostatics, we have

For any charge configuration, equipotential surface through a point is normal to the electric field. Justify.
Work done (W) in moving a test charge along an equipotential surface is zero.
Work done is given by, 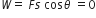
F is the electric force and s is the magnitude of displacement.
For non-zero displacement, this is possible only when cos  is equal to 0.
is equal to 0.
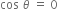
 = 90°
= 90°
Thus, the force acting on the point charge is perpendicular to the equipotential surface.
Electric field lines give us the direction of the electric force on a charge.
Thus, for any charge configuration, an equipotential surface through a point is normal to the electric field.
