The region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density ρ = A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is: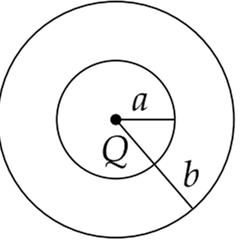

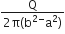
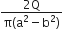
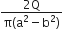
A.

A Gaussian surface at distance r from centre.
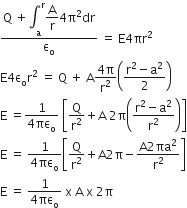
At the centre of the sphere is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is
As, Q = 2πAa2
i.e A = Q/2πa2
(a) An electric dipole of dipole moment p⃗ consists of point charges +q and –q separated by a distance 2a apart. Deduce the expression for the electric field E⃗ due to the dipole at a distance x from the center of the dipole on its axial line in terms of the dipole moment p⃗. Hence show that in the limit x >> a, E⃗ → 2 p⃗/ (4p ε0 x3).
(b) Given the electric field in the region E⃗ = 2x i, find the net electric flux through the cube and the charge enclosed by it.
Electric field on axial line of an electric dipole is given by, 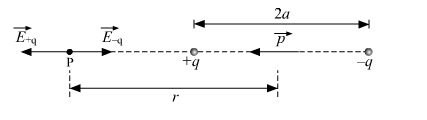
Suppose, P is a point at distance r from the center of the dipole on the side of charge –q.
Electric field at P due to –q is given by, ![]() is the unit vector along the dipole axis.
is the unit vector along the dipole axis.
Electric field at P due to +q is given by,![]()
Therefore, total electric field at point P is,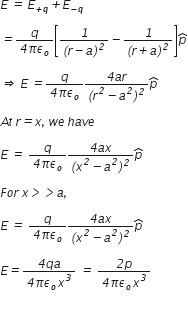
b) Since, the electric field is parallel to the faces parallel to xy and xz planes, the electric flux through them is zero.
Electric flux through the left face,
![]()
Using Gauss’ laws deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R. (r being the distance from the centre of the shell).
i) Consider a uniformly charged thin spherical shell of radius R carrying charge Q. To find the electric field outside the shell, we consider a spherical Gaussian surface of radius (r >R), concentric with given shell. If E is electric field outside the shell, then by symmetry electric field strength has same magnitude E0 on the Gaussian surface and is directed radially outward.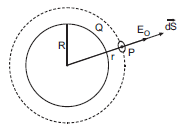
So, electric flux through Gaussian surface is given by, ![]()
Therefore, ![]()
Charge enclosed by the Gaussian surface is Q.
Therefore, using gauss’s theorem, we have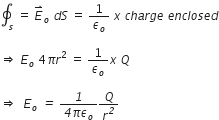
Thus, electric field outside a charged thin spherical shell is the same as if the whole charge Q is concentrated at the centre.
ii) Electric field inside the shell: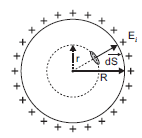
The charge resides on the surface of a conductor. Thus, a hollow charged conductor is equivalent to a charged spherical shell. Let’s consider a spherical Gaussian surface of radius (r < R). If E is the electric field inside the shell, then by symmetry electric field strength has the same magnitude Ei on the Gaussian surface and is directed radially outward.
Electric flux through the Gaussian surface is given by, ![]()
= ![]()
Now, Gaussian surface is inside the given charged shell, so charge enclosed by Gaussian surface is zero.
Therefore, using Gauss’s theorem, we have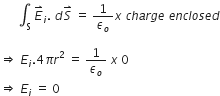
Thus, electric field at each point inside a charged thin spherical shell is zero.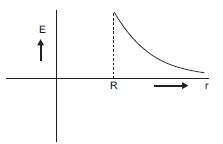
The graph above shows the variation of electric field as a function of R.
While travelling back to his residence in the car, Dr. Pathak was caught up in a thunderstorm. It became very dark. He stopped driving the car and waited for thunderstorm to stop. Suddenly he noticed a child walking alone on the road. He asked the boy at his residence. The boy insisted that Dr. Pathak should meet his parents. The parents expressed their gratitude to Dr. Pathak for his concern for safety of the child.
Answer the following questions based on the above information:
(a) Why is it safer to sit inside a car during a thunderstorm?
(b) Which two values are displayed by Dr. Pathak in his actions?
(c) Which values are reflected in parents’ response to Dr. Pathak?
(d) Give an example of a similar action on your part in the past from everyday life.
a) On the basis of electrostatic screening, no electric field exists inside the charged conducting body. During lightening a shower of the charged particles falls on the earth. So it would be safer to sit inside the car.
(b) Dr. Pathak knows the result of lightening during thunderstorm; so he displayed two actions;
(i) Shows love, kindness and sympathy to the child.
(ii) Keeping in view the safety of the child, he allow the boy to sit in the car till the thunderstorm stopped.
(c) Parent meets Dr. Pathak; and express their gratitude and heart felt thank for providing the safety to the child from lightning and thunderstorm.
(d) Many of us have read in the newspaper that the person either working in the field or in open space have lost their life during thunderstorm. So the persons belonging to villages must be given advices that they should remain inside the houses during thunderstorm.
(a) Define electric flux. Write its S.I. units.
(b) Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged?a) Electric flux is defined as the total number of electric field lines passing through an area normal to them.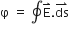
SI unit is Nm2/C.
b) Gauss’s theorem states that the total electric flux through a closed surface is equal to times the net charge enclosed by the surface. 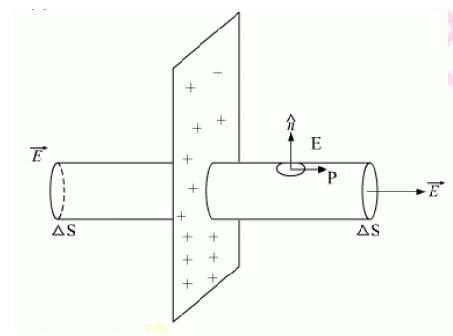
Consider a uniformly charged infinite plane sheet of charge density  .
.
Consider a Gaussian surface inside as shown in the figure which is in the form of a cylinder.
On applying Gauss’s law, we have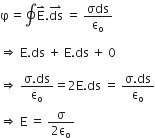
Thus, electric field strength due to an infinite flat sheet of charge is independent of the distance of the point and is directed normally away from the charge.
If the surface charge density s is negative the electric field is directed towards the surface charge.
c) i) Away from the charged sheet.
ii) towards the plane sheet.
