Given, 
Frequency band of radio = 7.5 MHz - 12 MHz

 $$\begin{gathered} \mathrm{Wavelength}, \boxed{{\mathrm{\lambda }}_1 = \frac{\mathrm{c}}{{\mathrm{v}}_1}} = \frac{3 \times {10}^8}{7.5 \times {10}^6} = 40 \mathrm{m} \\ \mathrm{Wavelength}, {\mathrm{\lambda }}_2 = \frac{\mathrm{c}}{{\mathrm{v}}_2} = \frac{3 \times {10}^8}{12 \times {10}^6} = 25 \mathrm{m} \end{gathered}$$ 

Therefore, the corresponding wavelength band is 40 m - 25 m.

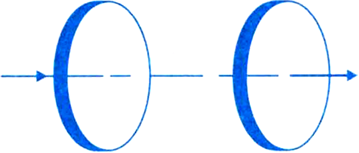
(a) Given,
Radius of capacitor plates, r = 12 cm = 0.12 m

distance between the plates, d = 5.0 mm = 5 × 10^-3m

Charge carried, I = 0.15 A

Permittivity of medium, $\mathrm{\epsilon }$₀ = 8.85 × 10^-12 C² N^-1 m²

∴ Area of cross-section of plates, A = $\mathrm{\pi }$R² = 3.14 × (0.12)² m² 

Capacitance of parallel plate capacitor is given by
                        ^{$$\begin{gathered} \boxed{\mathrm{C} = \frac{{\mathrm{\epsilon }}_0\mathrm{A}}{\mathrm{d}}} \\ = \frac{8.85 \times {10}^{-12}\times (3.14) \times (0.12{)}^2}{5 \times {10}^{-3}} \\ = 80.1 \times {10}^{-12} = 80.1 \mathrm{pF} \end{gathered}$$}

Now, charge on capacitor plate, $\boxed{\mathrm{q} = \mathrm{CV}}$ 

     $\Rightarrow$           $\frac{\mathrm{dq}}{\mathrm{dt}} = \mathrm{C} \times \frac{\mathrm{dV}}{\mathrm{dt}}$

$\Rightarrow$                     $\mathrm{I} = \mathrm{C} \times \frac{\mathrm{dV}}{\mathrm{dt}} \left[\because \mathrm{I} = \frac{\mathrm{dq}}{\mathrm{dt}}\right]$ 

$\Rightarrow$                        $\frac{\mathrm{dV}}{\mathrm{dt}} = \frac{\mathrm{I}}{\mathrm{C}} = \frac{0.15}{80.1 \times {10}^{-12}}$

                           $= 1.87 \times {10}^9\hspace{0.17em}{\mathrm{Vs}}^{-1}$ 

(b) Displacement current is equal to the conduction current i.e., 0.15 A.

(c) Yes, Kirchhoff's first rule is valid at each plate of the capacitor provided. We take the current to be the sum of the conduction and displacement currents.

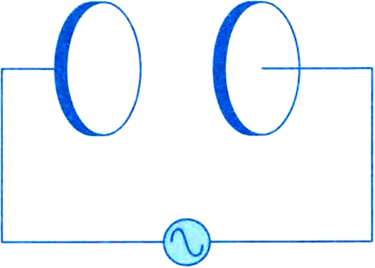
Given, a parallel plate capacitor made of circular plates.

(a) Here,
Radius of the circular plate, R = 6.0 cm
 $$\begin{gathered} \mathrm{Capacitance} \mathrm{of} \mathrm{the} \mathrm{plates}, \mathrm{C} = 100 \mathrm{\rho F} = 100 \times {10}^{-12}\mathrm{F} \\ \mathrm{Angular} \mathrm{frequency}, \mathrm{\omega } = 300 \mathrm{rad} {\mathrm{s}}^{-1} \end{gathered}$$

${\mathrm{E}}_{\mathrm{rms}} = 230 \mathrm{V}$

Therefore, 

           $\boxed{{\mathrm{I}}_{\mathrm{rms}} = \frac{{\mathrm{E}}_{\mathrm{rms}}}{{\mathrm{X}}_{\mathrm{C}}}} = \frac{{\mathrm{E}}_{\mathrm{rms}}}{{\displaystyle \frac{1}{\mathrm{\omega C}}}} = {\mathrm{E}}_{\mathrm{rms}} \times \mathrm{\omega C}$ 

$\therefore$        ${\mathrm{I}}_{\mathrm{rms}} = 230 \times 300 \times 100 \times {10}^{-12}$
                 $= 6.9 \times {10}^{-6}\mathrm{A} = 6.9 \mathrm{\mu A}$ 

(b) Yes, the conduction current is equal to the displacement current.

$$\begin{gathered} \mathrm{I} = {\mathrm{I}}_{\mathrm{D}}, \mathrm{whether} \mathrm{conduction} \mathrm{current}, \mathrm{I} \mathrm{is} \mathrm{steady} \mathrm{d}.\mathrm{c}. \mathrm{or} \mathrm{a}.\mathrm{c}. \\ \mathrm{This} \mathrm{can} \mathrm{be} \mathrm{shown} \mathrm{below} : \end{gathered}$$

          $\boxed{{\mathrm{I}}_{\mathrm{D}} = {\mathrm{\epsilon }}_0\frac{\mathrm{d}\left({\mathrm{\varphi }}_{\mathrm{E}}\right)}{\mathrm{dt}}} = {\mathrm{\epsilon }}_0 \frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{EA}\right)$     $\left(\therefore {\mathrm{\varphi }}_{\mathrm{E}} = \mathrm{EA}\right)$

$\Rightarrow$      ${\mathrm{I}}_{\mathrm{D}} = {\mathrm{\epsilon }}_0\mathrm{A}\frac{\mathrm{dE}}{\mathrm{dt}}$
            $= {\mathrm{\epsilon }}_0\mathrm{A}\frac{\mathrm{d}}{\mathrm{dt}}\left(\frac{\mathrm{Q}}{{\mathrm{\epsilon }}_0\mathrm{A}}\right)$      $\left(\because \mathrm{E} = \frac{\mathrm{\sigma }}{{\mathrm{\epsilon }}_0} = \frac{\mathrm{Q}}{{\mathrm{\epsilon }}_0\mathrm{A}}\right)$ 
$\Rightarrow$     $$\begin{gathered} {\mathrm{I}}_{\mathrm{D}} = {\mathrm{\epsilon }}_0\mathrm{A} \times \frac{1}{{\mathrm{\epsilon }}_0\mathrm{A}}\frac{\mathrm{dQ}}{\mathrm{dt}} \\ = \frac{\mathrm{dQ}}{\mathrm{dt}} = \mathrm{I} \end{gathered}$$
(c) We know that, 

                      $\boxed{\mathrm{B} = \frac{{\mathrm{\mu }}_0}{2\mathrm{\pi }}\frac{\mathrm{r}}{{\mathrm{R}}^2}{\mathrm{I}}_{\mathrm{D}}}$ 

This formula goes through even if displacement current, I_D (and therefore magnetic field B) oscillates in time. The formula above shows that they oscillate in phase.
Since I_D = I, we have
                      $\mathrm{B} = \frac{{\mathrm{\mu }}_0\mathrm{rI}}{2{\mathrm{\pi R}}^2}$ 

If I = I₀, the maximum value of current, then
Amplitude of B = maximum value of B 

$$\begin{gathered} = \frac{{\mathrm{\mu }}_0{\mathrm{rI}}_0}{2{\mathrm{\pi R}}^2} = \frac{{\mathrm{\mu }}_0\mathrm{r}\sqrt{2}{\mathrm{I}}_{\mathrm{rms}}}{2{\mathrm{\pi R}}^2} \left(\because {\mathrm{I}}_0 = \sqrt{2} {\mathrm{I}}_{\mathrm{rms}}\right) \\ = \frac{4\mathrm{\pi } \times {10}^{-7} \times 0.03 \times \sqrt{2} \times 6.9 \times {10}^{-6}}{2 \times 3.14 \times (0.06{)}^2}\mathrm{T} \\ = 1.63 \times {10}^{-11}\mathrm{T}. \end{gathered}$$