Hydrogen (1H1), deuterium (1H2), singly ionised helium (2He4+) and doubly ionised lithium (3Li8)2+ all have one electron around the nucleus. Consider an electron transition from n =2 to n=1. If the wavelengths of emitted radiation are λ1,λ2,λ3 andλ4, respectively for four elements, then approximately which one of the following is correct?
4λ1=2λ2=2λ3 =λ4
λ1=2λ2=2λ3 =λ4
λ1=λ2=4λ3 =9λ4
λ1=λ2=4λ3 =9λ4
C.
λ1=λ2=4λ3 =9λ4
For hydrogen atom, we get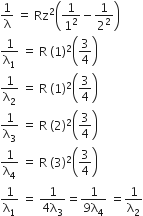
In a hydrogen like atom, electron makes the transition from an energy level with quantum number n to another with a quantum number (n – 1). If n >> 1, the frequency of radiation emitted is proportional to
1/n
1/n2
1/n3/2
1/n3/2
D.
1/n3/2
An energy gap, ΔE = hv
Here, h is Planck's constant
therefore,
Frequency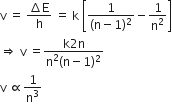
The radiation corresponding to 3 → 2 transition of hydrogen atom falls on a metal surface to produce photoelectrons. These electrons are made to enter a magnetic field of 3 x 10-4 T. If the radius of the largest the circular path followed by these electrons is 10.0 mm, the work function of the metal is close to:
1.8 eV
1.1 eV
0.8 eV
0.8 eV
B.
1.1 eV
mv =qBR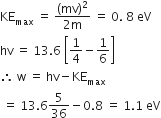
Using Bohr’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number ni ) to the lower state, (nf ).
When electron in hydrogen atom jumps from energy state ni =4 to nf =3, 2, 1, identify the spectral series to which the emission lines belong.
According to Bohr’s postulates, in a hydrogen atom, a single electron revolves around a nucleus of charge +e. For an electron moving with a uniform speed in a circular orbit on a given radius, the centripetal force is provided by the Coulomb force of attraction between the electron and the nucleus.
Therefore, 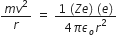 ... (1)
... (1) 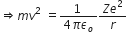
So, Kinetic Energy, K.E = 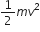
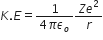
Potential energy is given by, P.E = 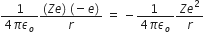
Therefore, total energy is given by, E = K.E + P.E = 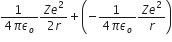
E = 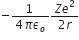 , is the total energy.
, is the total energy.
For nth orbit, E can be written as En,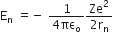 ... (2)
... (2)
Now, using Bohr's postulate for quantization of angular momentum, we have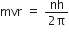
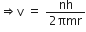
Putting this value of v in equation (1), we get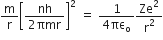
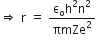
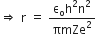
Now, putting value of rn in equation (2), we get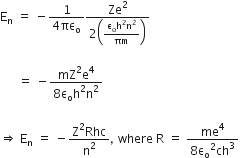
R is the rydberg constant.
For hydrogen atom Z =1,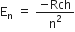
If ni and nf are the quantum numbers of initial and final states and Ei & Ef are energies of electron in H-atom in initial and final state, we have 

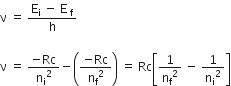
That is, when electron jumps from ni = 4 to nf = 3.21 .
Radiation belongs to Paschen, Balmer, and Lyman series.
As an electron makes a transition from an excited state to the ground state of a hydrogen – like atom/ion:
kinetic energy, potential energy and total energy decrease
kinetic energy decreases, potential energy increases but total energy remains same
kinetic energy and total energy decrease but potential energy increases
kinetic energy and total energy decrease but potential energy increases
A.
kinetic energy, potential energy and total energy decrease
As we know that kinetic energy of an electron is
KE ∝ (Z/n)2
when the electron makes the transition from an excited state of the ground state then n, decreases and KE increases. We know that PE is lowest for the ground state. As TE=- KE and TE also decreases.
